Razão e Proporção

Razão e Proporção — Guia Completo com Exemplos e Exercícios

Razão e Proporção: guia prático com exemplos e exercícios

Aprenda o que é razão, o que é proporção, como aplicar o produto dos meios e dos extremos e resolver problemas clássicos. Linguagem simples, contas “uma embaixo da outra” e soluções em abre/fecha.

🔖 Reforço rápido: Mapas Mentais de Matemática • ENEM Matemática • Pacote 10 eBooks • Banco de Questões • E-book de Fórmulas (GRÁTIS)

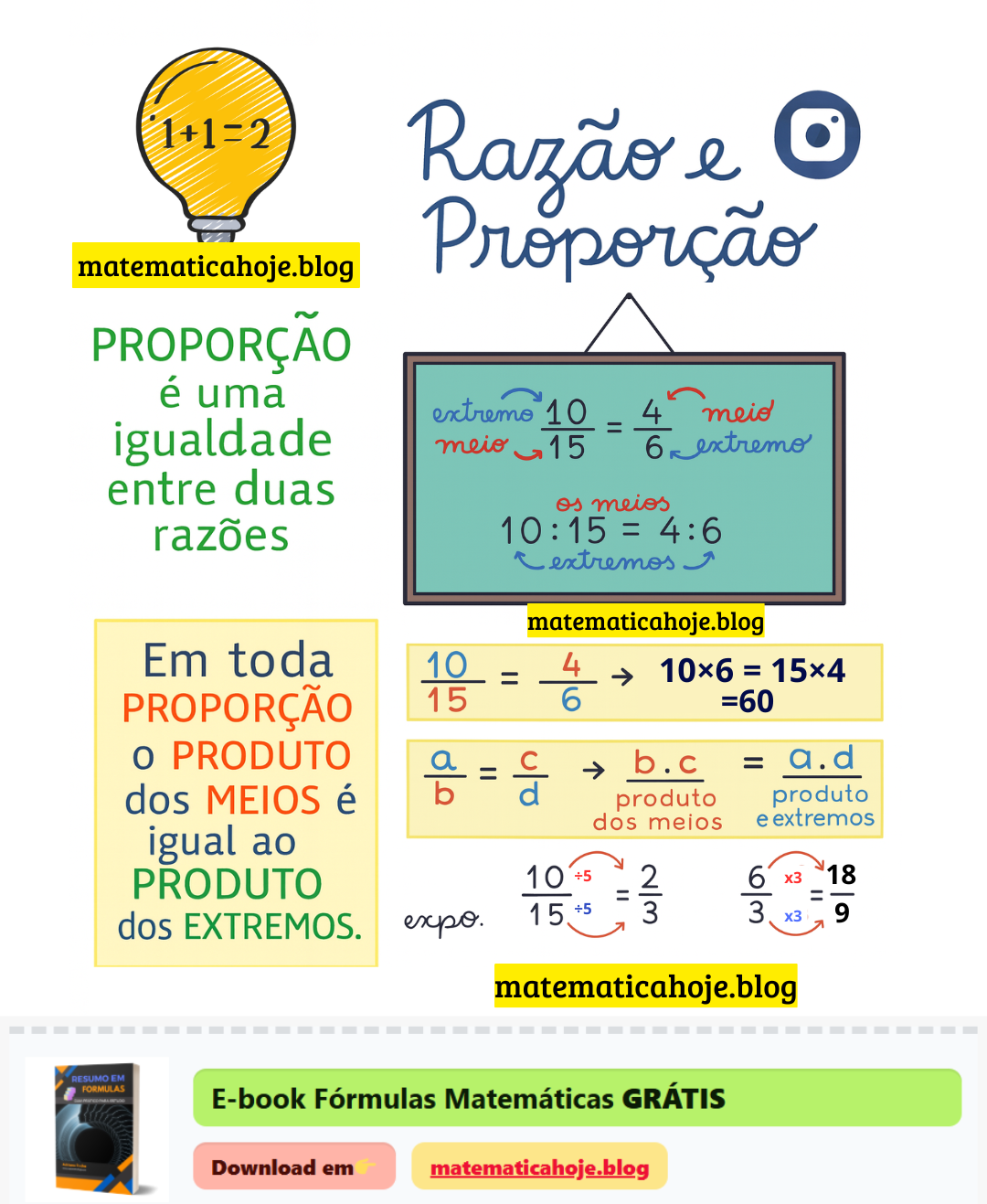
O que é Razão?

Razão é a comparação entre grandezas do mesmo tipo por meio de uma divisão. Se \(a\) e \(b\) são números reais com \(b\neq 0\), então a razão entre \(a\) e \(b\) é \(\dfrac{a}{b}\) (ou \(a:b\)).

Exemplo (simplificação)
\[ \frac{10}{15}=\frac{2}{3} \] \[ 10\div 5 = 2 \\ 15\div 5 = 3 \]

Dica: antes de comparar razões, simplifique ambas. Razões equivalentes representam a mesma proporção.

O que é Proporção?

Proporção é uma igualdade entre duas razões. Ex.: \(\dfrac{10}{15}=\dfrac{4}{6}\). Em toda proporção, o produto dos meios é igual ao produto dos extremos.

\[ \frac{a}{b}=\frac{c}{d} \;\Rightarrow\; a\cdot d = b\cdot c \]

Exemplos resolvidos (linha a linha)

Exemplo 1 — Verificar se há proporção

\[ \frac{10}{15} \stackrel{?}{=} \frac{4}{6} \]

\[ 10\cdot 6 = 15\cdot 4 \\ 60 = 60 \]

Conclusão: é proporção.

Exemplo 2 — Encontrar termo faltante

Dado \(\dfrac{a}{15}=\dfrac{4}{6}\), determine \(a\).

\[ \frac{a}{15}=\frac{4}{6} \\ 6a = 15\cdot 4 \\ 6a = 60 \\ a = 10 \]

📚 Fortaleça a revisão

Baixar e-book de Fórmulas (GRÁTIS) Ver Mapas Mentais Praticar no Banco de Questões

Passo a passo para resolver proporções

Escreva a igualdade entre as razões.
Aplique \(a\cdot d = b\cdot c\).
Resolva a equação e simplifique o resultado.

Exercícios discursivos

Discursivo 1 — Escala

Um mapa usa escala \(1:50\,000\). A distância real é \(35\,km\). Qual a distância no mapa (em cm)?

👀 Mostrar solução

\[ 1:50\,000 = x:3\,500\,000 \text{ (cm)} \\ 50\,000\cdot x = 3\,500\,000 \\ x = \frac{3\,500\,000}{50\,000} \\ x = 70 \text{ cm} \]

Discursivo 2 — Receita

Uma receita pede farinha:açúcar \(= 3:2\). Para \(750\,g\) de farinha, quantos gramas de açúcar?

👀 Mostrar solução

\[ \frac{3}{2}=\frac{750}{x} \\ 3x=2\cdot 750 \\ 3x=1500 \\ x=500\,g \]

Exercícios de múltipla escolha

(MC) 1 — Produto dos meios e dos extremos

Se \(\dfrac{x}{14}=\dfrac{6}{7}\), então \(x\) é:

👀 Mostrar solução

\[ \frac{x}{14}=\frac{6}{7} \\ 7x = 14\cdot 6 \\ 7x = 84 \\ x = 12 \]

(MC) 2 — Razão equivalente

Qual razão é equivalente a \(\dfrac{8}{12}\)?

\(\dfrac{6}{8}\)
\(\dfrac{12}{20}\)
\(\dfrac{2}{3}\)
\(\dfrac{5}{9}\)

👀 Mostrar solução

\[ \frac{8}{12}=\frac{8\div4}{12\div4} \\ = \frac{2}{3} \]

(MC) 3 — Proporção inversa

Uma equipe com 5 pessoas conclui um serviço em 12 dias. Em quantos dias 8 pessoas fazem o mesmo serviço?

18
7,5
6
8

👀 Mostrar solução

\[ 5\cdot 12 = 8\cdot d \\ 60 = 8d \\ d = \frac{60}{8} \\ d = 7{,}5 \text{ dias} \]

Continue estudando

Palavras-chave relacionadas: matemática básica, operações com números inteiros, regras de sinais, adição e subtração de inteiros, multiplicação e divisão com sinais, jogo de sinais, proporção direta e inversa.

Conclusão

Razão compara grandezas; proporção iguala duas razões. Aplicando \(a\cdot d=b\cdot c\) e escrevendo os passos “um embaixo do outro”, você resolve problemas com segurança. Pratique bastante e consulte os resumos quando precisar.

Convite: baixe o E-book de Fórmulas gratuito, use os Mapas Mentais e siga nosso canal no WhatsApp para receber materiais e avisos.

Relacionadas

Matemática para Concursos: Números Decimais – Banca IBFC – Nível Médio

Razão e Proporção – Concurso Joinville 2024 – Banca CESPE

Matemática para Concursos: Razão e Proporção – Banca VUNESP - Nível Médio

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.