Redução ao 1º Quadrante: 2º, 3º e 4º
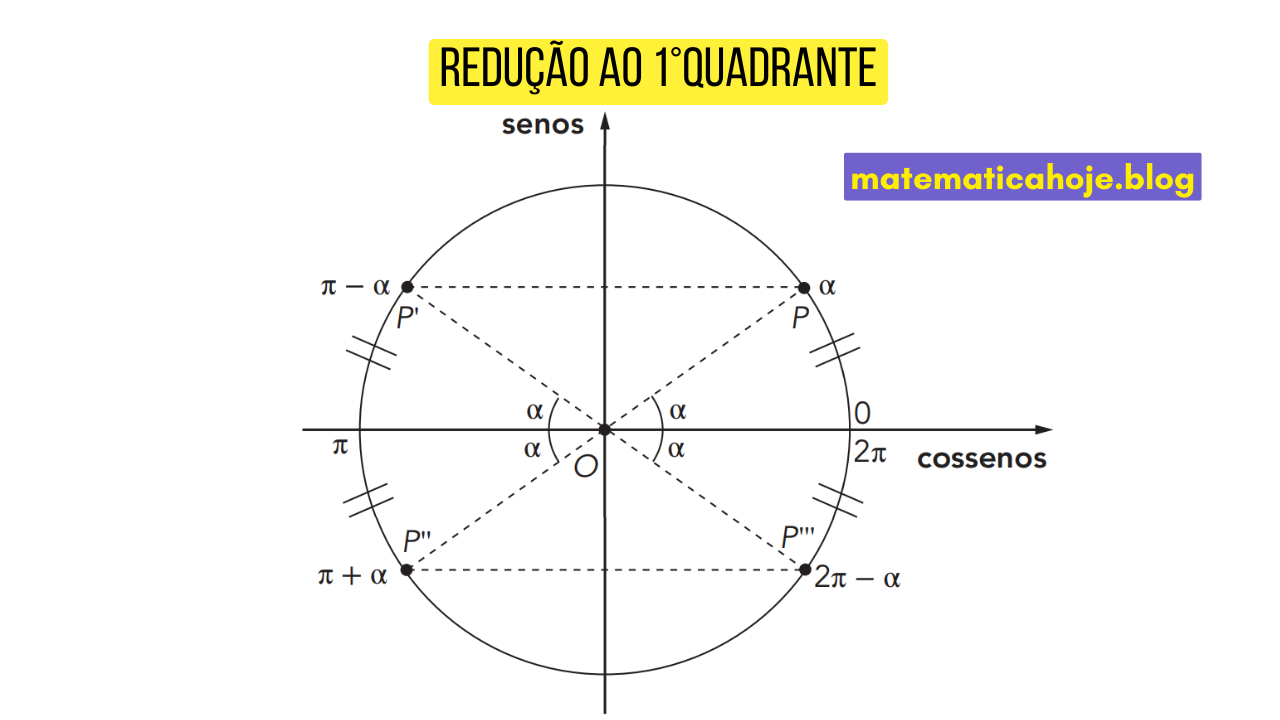
Reduzir um ângulo \(\theta\) a um ângulo de referência \( \alpha \in (0,\tfrac{\pi}{2}) \) simplifica o cálculo de \(sen\theta\) e \(\cos\theta\). Abaixo você encontra, para cada quadrante, a imagem de apoio e os exemplos com as **contas alinhadas verticalmente**.
2º quadrante → 1º
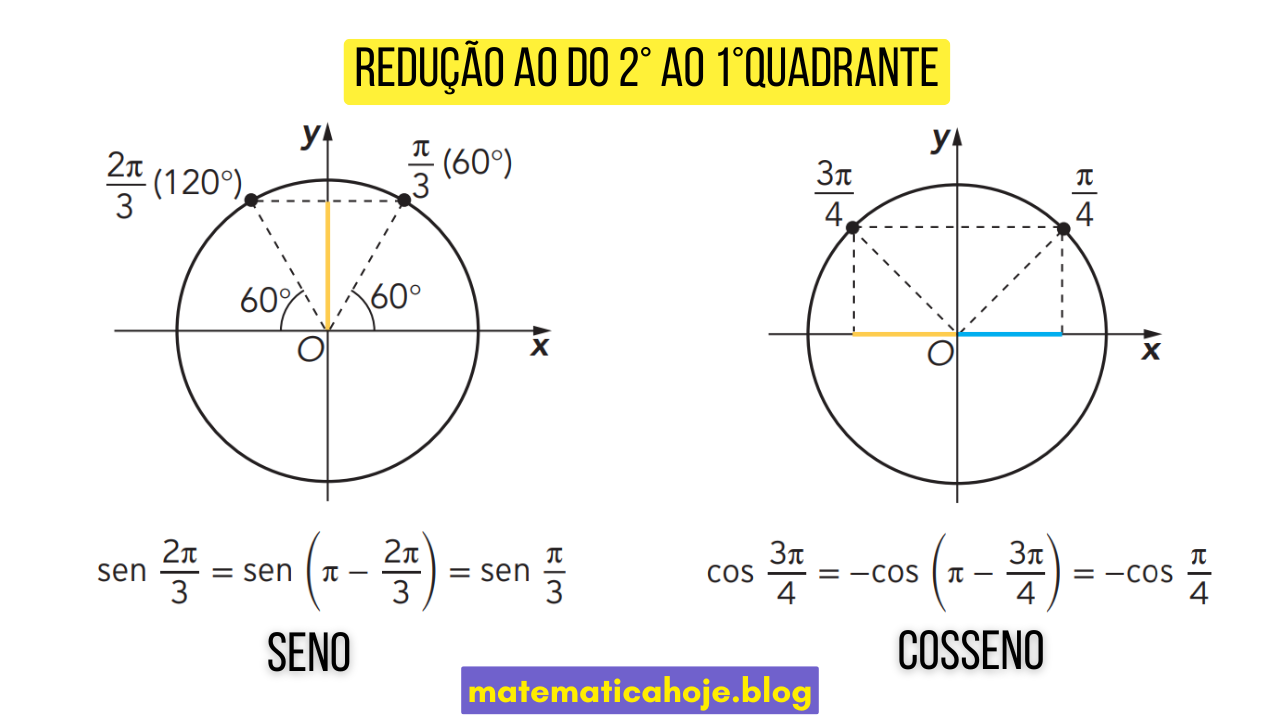
Exemplo (em graus)
Calcule \(sen(150^\circ)\) e \(\cos(150^\circ)\).
3º quadrante → 1º
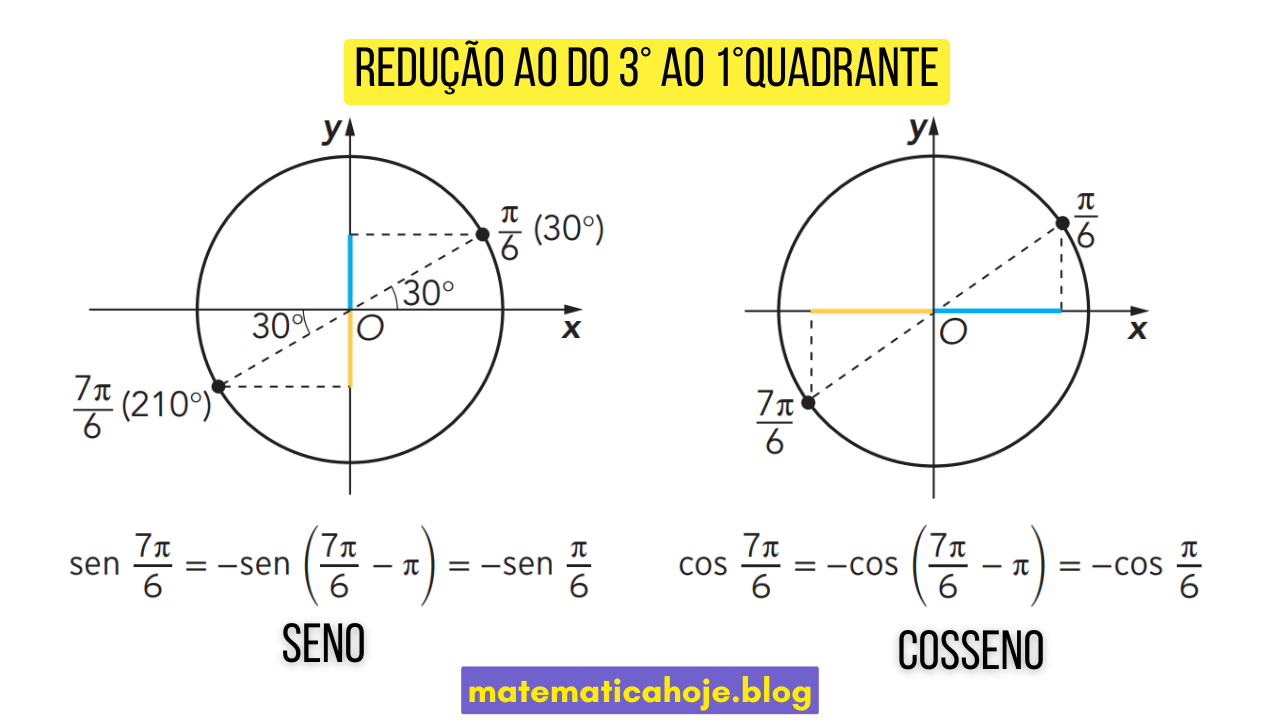
Exemplo (em radianos)
Calcule \(sen\!\left(\tfrac{7\pi}{6}\right)\) e \(\cos\!\left(\tfrac{7\pi}{6}\right)\).
4º quadrante → 1º
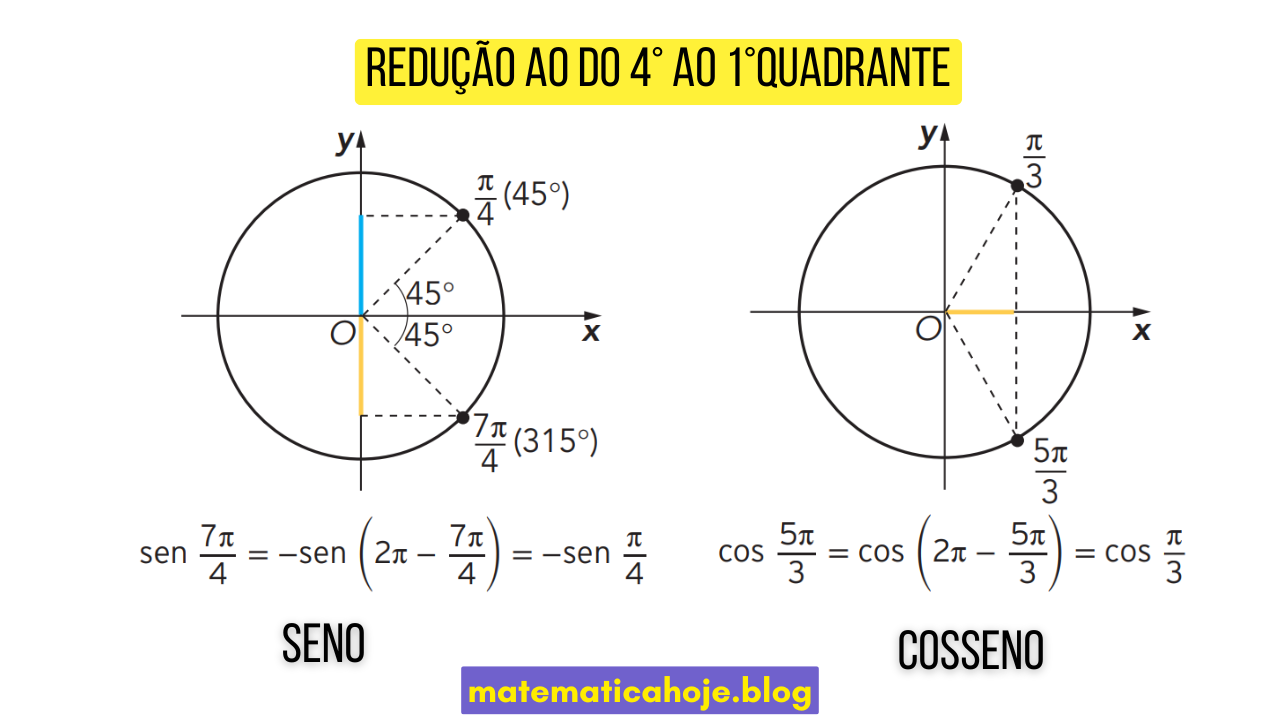
Exemplo (em graus)
Calcule \(sen(330^\circ)\) e \(\cos(330^\circ)\).
Exercícios rápidos
1) \(\cos(120^\circ)=\)
Ver solução
2) \(sen\!\left(\tfrac{11\pi}{6}\right)=\)
Ver solução
3) \(\cos\!\left(\tfrac{7\pi}{6}\right)=\)
Ver solução
📝 Exercícios de múltipla escolha
Exercício 1. Calcule \(sen(150^\circ)\).
- A) \(-\tfrac{\sqrt{3}}{2}\)
- B) \(-\tfrac{1}{2}\)
- C) \(\tfrac{1}{2}\)
- D) \(\tfrac{\sqrt{3}}{2}\)
- E) \(1\)
Ver solução
Resposta correta: C
Exercício 2. O valor de \(\cos\!\left(\tfrac{7\pi}{6}\right)\) é:
- A) \(-\tfrac{\sqrt{3}}{2}\)
- B) \(-\tfrac{1}{2}\)
- C) \(\tfrac{1}{2}\)
- D) \(\tfrac{\sqrt{3}}{2}\)
- E) \(0\)
Ver solução
Resposta correta: A
Exercício 3. O valor de \(sen(330^\circ)\) é:
- A) \(-\tfrac{1}{2}\)
- B) \(\tfrac{1}{2}\)
- C) \(\tfrac{\sqrt{3}}{2}\)
- D) \(-\tfrac{\sqrt{3}}{2}\)
- E) \(0\)
Ver solução
Resposta correta: A






















