(CESPE / CEBRASPE 2005 – TRE-MT – Analista Judiciário)
Tendo em vista a exigência de realização de uma tarefa determinada pelo Tribunal Superior Eleitoral, verificou-se que, com os dez servidores de um determinado setor, trabalhando oito horas por dia, seriam necessários quinze dias para o atendimento da referida demanda. Dada a necessidade de sua conclusão em doze dias, e mediante a prorrogação da jornada dos servidores alocados à tarefa para dez horas, o número de servidores a mais que deveriam ser colocados à disposição para a realização do trabalho é igual a
A) dez.
B) oito.
C) cinco.
D) dois.
E) zero.
Vamos resolver o problema utilizando regra de três composta, que é apropriada quando há várias variáveis relacionadas ao trabalho, como número de servidores, horas de trabalho e dias.
Passo 1: Identificação das grandezas envolvidas
Temos três grandezas relacionadas:
- Número de servidores (S): Quanto mais servidores, menos dias são necessários.
- Horas por dia (H): Quanto mais horas por dia, menos dias são necessários.
- Número de dias (D): Quanto menos dias, mais servidores ou mais horas são necessários.
Passo 2: Montando a relação inicial
Dados iniciais:
- 10 servidores trabalhando 8 horas por dia durante 15 dias completariam a tarefa.
- Queremos saber quantos servidores são necessários para realizar o mesmo trabalho em 12 dias, com uma jornada de 10 horas por dia.
Vamos utilizar a regra de três composta para resolver:
| Servidores | Horas/dia | Dias |
|---|---|---|
| 10 | 8 | 15 |
| ( x ) | 10 | 12 |
Passo 3: Analisando as relações
- Servidores vs. dias: Quanto menos dias disponíveis, mais servidores são necessários (grandeza inversamente proporcional).
- Servidores vs. horas/dia: Quanto mais horas por dia trabalhadas, menos servidores são necessários (grandeza inversamente proporcional).
Passo 4: Montando a regra de três composta
Como estamos lidando com grandezas inversamente proporcionais, para montar a equação, vamos inverter os valores das grandezas que têm relação inversa com o número de servidores.
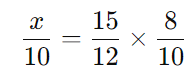
Passo 5: Resolvendo a equação
Primeiro, resolvemos as frações:
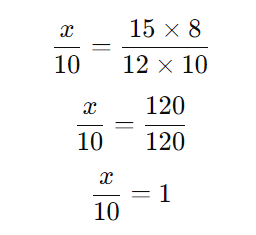
Multiplicando ambos os lados por 10:
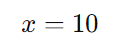
Passo 6: Conclusão
A quantidade de servidores necessários é 10, ou seja, não é necessário adicionar mais servidores. Logo, a resposta correta é a Alternativa E: zero.













