A regra de três simples é uma técnica da matemática básica utilizada para resolver problemas que envolvem duas grandezas que são proporcionais entre si. Quando temos uma situação em que duas grandezas são diretamente ou inversamente proporcionais, podemos usar essa regra para encontrar um valor desconhecido. Neste artigo, vamos entender o conceito da regra de três simples, aprender como aplicá-la e resolver alguns exemplos práticos.
O Que é Regra de Três Simples?
A regra de três simples é utilizada para encontrar um valor desconhecido a partir de três valores conhecidos que mantêm uma relação de proporcionalidade. Essa relação pode ser direta ou inversa.
- Proporcionalidade Direta: Quando uma grandeza aumenta, a outra também aumenta na mesma proporção, e quando uma diminui, a outra também diminui.
- Proporcionalidade Inversa: Quando uma grandeza aumenta, a outra diminui na mesma proporção e vice-versa.
Como Montar uma Regra de Três Simples?
Para aplicar a regra de três simples, siga os seguintes passos:
- Identifique as grandezas envolvidas e determine se são diretamente ou inversamente proporcionais.
- Organize os dados em uma tabela, relacionando cada grandeza com o seu valor correspondente.
- Monte a proporção e resolva a equação para encontrar o valor desconhecido.
Exemplo 1: Proporcionalidade Direta
Problema:
Um carro percorre 150 km com 10 litros de combustível. Quantos litros de combustível são necessários para percorrer 300 km?
Passo a Passo:
- Identifique as grandezas envolvidas:
- Distância (km)
- Combustível (litros)
- Como a distância percorrida aumenta, a quantidade de combustível necessária também aumenta. Portanto, é uma proporcionalidade direta.
- Organize os dados na forma de uma tabela:
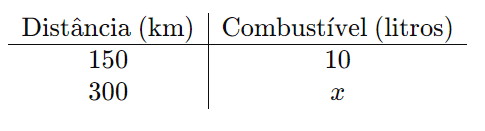
- Monte a proporção e resolva:
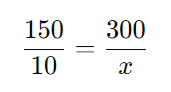
Multiplicando em cruz:

Resposta: São necessários 20 litros de combustível para percorrer 300 km.
Exemplo 2: Proporcionalidade Inversa
Problema:
Três operários constroem um muro em 12 dias. Em quantos dias 4 operários, trabalhando na mesma intensidade, constroem o mesmo muro?
Passo a Passo:
- Identifique as grandezas envolvidas:
- Número de operários
- Tempo (dias)
- Quanto maior o número de operários, menor será o tempo necessário para construir o muro. Portanto, é uma proporcionalidade inversa.
- Organize os dados na forma de uma tabela:

- Monte a proporção invertida e resolva:
Resposta: 4 operários constroem o muro em 9 dias.
Exemplo 3: Situação Cotidiana
Problema:
Uma torneira enche um tanque com 500 litros de água em 8 horas. Quantos litros ela encherá em 3 horas?
Passo a Passo:
- Identifique as grandezas envolvidas:
- Tempo (horas)
- Volume (litros)
- Como o tempo de fluxo diminui, o volume de água coletado também diminui. Portanto, é uma proporcionalidade direta.
- Organize os dados na forma de uma tabela:
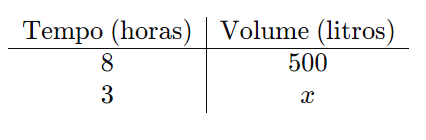
- Monte a proporção e resolva:
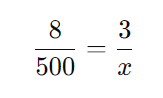
Multiplicando em cruz:
Resposta: A torneira encherá 187,5 litros em 3 horas.
Conclusão
A regra de três simples é uma ferramenta poderosa e prática para resolver problemas do cotidiano que envolvem grandezas proporcionais. Compreender quando aplicar proporcionalidade direta ou inversa é essencial para garantir cálculos corretos e eficientes.
Espero que este artigo tenha ajudado você a entender a regra de três simples! Se tiver alguma dúvida ou quiser mais exemplos, deixe seu comentário!

























