1) Conceito central: funções inversas
A função exponencial \( f(x)=a^x \) (com \( a>0 \) e \( a\neq 1 \)) tem como inversa a função logarítmica \( f^{-1}(x)=\log_a x \). Essa inversão produz a equivalência:
\( \displaystyle a^x=b \quad \Longleftrightarrow \quad x=\log_a b \).
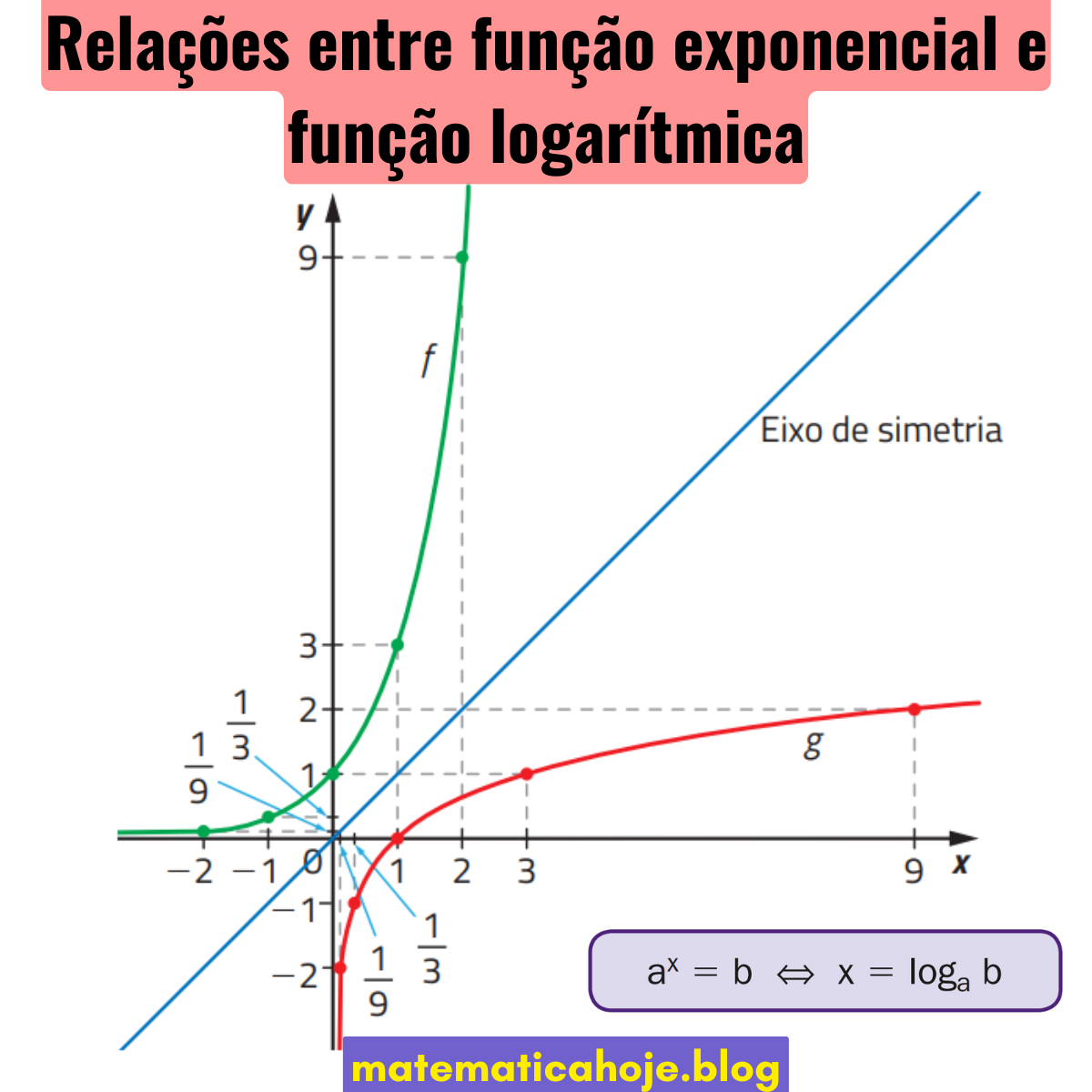
2) Relação entre os gráficos
3) Propriedades “espelho” (composição)
Identidades fundamentais:
- \( \displaystyle a^{\log_a x}=x \) para \( x>0 \) (exponencial “desfaz” o logaritmo).
- \( \displaystyle \log_a(a^x)=x \) para \( x\in \mathbb{R} \) (logaritmo “desfaz” a exponenciação).
Essas igualdades são o coração das trocas entre as formas exponencial e logarítmica.
4) Exemplos resolvidos
Exemplo 1 — Converta \( a^{2x-1}=8 \) para forma logarítmica e resolva (suponha \( a=2 \)).
\( 2^{2x-1}=8=2^3 \Rightarrow 2x-1=3 \Rightarrow x=2 \). Em forma logarítmica: \( 2x-1=\log_2 8 = 3 \).
Exemplo 2 — Resolva \( \log_3(x-1)=2 \).
Pela equivalência, \( x-1=3^2=9 \Rightarrow x=10 \) (válido pois \(x>1\)).
Exemplo 3 — Calcule \( 2^{\log_2 9} \).
Use \( a^{\log_a b}=b \Rightarrow 2^{\log_2 9}=9 \).
Exemplo 4 — Ache a inversa de \( f(x)=a^x \) e descreva domínio e imagem.
Troque \( x \leftrightarrow y \): \( x=a^y \Rightarrow y=\log_a x \). Logo \( f^{-1}(x)=\log_a x \), com domínio \( (0,\infty) \) e imagem \( \mathbb{R} \).
5) Exercícios de múltipla escolha
1) Se \( a>1 \), assinale a alternativa correta:
- a) \( a^x \) é crescente e \( \log_a x \) é decrescente
- b) Ambos são crescentes
- c) Ambos são decrescentes
- d) \( a^x \) é decrescente e \( \log_a x \) é crescente
Ver solução
Para \( a>1 \), os dois são crescentes. Alternativa b.
2) A inversa de \( f(x)=2^x \) é:
- a) \( 2^{-x} \)
- b) \( \log_2 x \)
- c) \( \ln x \)
- d) \( e^x \)
Ver solução
\( f^{-1}(x)=\log_2 x \). Alternativa b.
3) Resolva \( \log_{1/3}(x)=-2 \).
- a) \( x=\tfrac{1}{9} \)
- b) \( x=3 \)
- c) \( x=9 \)
- d) \( x=\tfrac{1}{3} \)
Ver solução
\( x=(1/3)^{-2}=9 \). Alternativa c.
4) Qual afirmação é verdadeira?
- a) O gráfico de \( \log_a x \) é a reflexão de \( a^x \) em torno do eixo \(x\)
- b) O gráfico de \( \log_a x \) é a reflexão de \( a^x \) em torno da reta \( y=x \)
- c) O gráfico de \( \log_a x \) é a translação de \( a^x \)
- d) Nenhuma das anteriores
Ver solução
São inversas; reflete-se na reta \( y=x \). Alternativa b.
5) Complete: \( \displaystyle a^{\log_a(5)}=\ \) ?
- a) \( \log_a(5) \)
- b) \( 5 \)
- c) \( a \)
- d) \( \ln 5 \)
Ver solução
Pela identidade \( a^{\log_a b}=b \Rightarrow 5 \). Alternativa b.
6) A assíntota da exponencial \( y=a^x \) (com \( a>0,\ a\neq1 \)) e a da logarítmica \( y=\log_a x \) são, respectivamente:
- a) \( y=0 \) e \( x=0 \)
- b) \( x=0 \) e \( y=0 \)
- c) \( y=1 \) e \( x=1 \)
- d) não possuem assíntotas
Ver solução
Exponencial: assíntota horizontal \( y=0 \). Logarítmica: assíntota vertical \( x=0 \). Alternativa a.
