Reta Tangente e Secante — Guia Completo
Aprenda o que são retas tangente e secante, suas fórmulas, aplicações práticas e como elas se conectam ao conceito de derivada. Inclui exemplos resolvidos passo a passo e exercícios com soluções.
1) Conceito de Reta Tangente
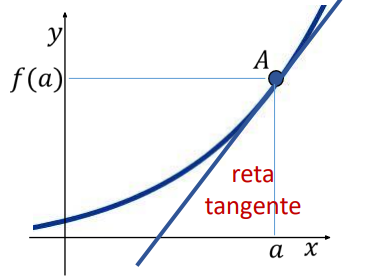
A reta tangente a uma curva em um ponto \(P\) é a reta que toca a curva nesse ponto e tem a mesma inclinação que a curva naquele instante:
\(m = f'(x_0)\)
Logo, a equação da reta tangente no ponto \(P(x_0, y_0)\) é:
\(y – y_0 = f'(x_0)(x – x_0)\)
2) Conceito de Reta Secante
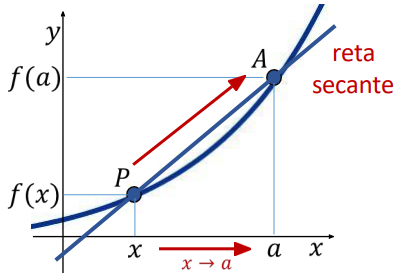
A reta secante passa por dois pontos distintos da curva e representa a inclinação média entre eles:
\(m = \dfrac{f(x_2)-f(x_1)}{x_2-x_1}\)
3) Relação entre Tangente, Secante e Derivada
Sejam \(P(x_0, f(x_0))\) e \(Q(x_0+h, f(x_0+h))\) na curva:
- Secante: Inclinação média: \(\dfrac{f(x_0+h)-f(x_0)}{h}\).
- Tangente: Limite da inclinação da secante quando \(Q \to P\):
\(m = \lim\limits_{h \to 0} \dfrac{f(x_0+h)-f(x_0)}{h} = f'(x_0)\)
Resumo: A tangente é um caso limite da secante quando os dois pontos se aproximam.
4) Exemplos Resolvidos
Exemplo 1 — Equação da reta tangente
Enunciado: Encontre a equação da reta tangente à curva \(f(x)=x^2\) no ponto \(P(2,4)\).
Passo 1: \(f'(x)=2x \Rightarrow m=f'(2)=4\).
Passo 2: \(y-4=4(x-2)\Rightarrow \boxed{y=4x-4}\).
Exemplo 2 — Equação da reta secante
Enunciado: Encontre a reta secante à curva \(f(x)=x^2\) passando por \(A(1,1)\) e \(B(3,9)\).
Passo 1: \(m=\dfrac{9-1}{3-1}=\dfrac{8}{2}=4\).
Passo 2: Usando \(A(1,1)\): \(y-1=4(x-1)\Rightarrow \boxed{y=4x-3}\).
5) Exercícios Propostos
Pratique para consolidar os conceitos de tangentes e secantes:
- Determine a equação da reta tangente à curva \(f(x)=x^3\) no ponto \(P(1,1)\).
- Encontre a equação da reta secante à curva \(f(x)=\sqrt{x}\) passando por \((1,1)\) e \((4,2)\).
- Mostre que, para \(f(x)=x^2+2x\), a inclinação da tangente em \(x=1\) é o limite da inclinação da secante quando os pontos se aproximam.
- Para \(f(x)=\ln(x)\), encontre a equação da reta tangente no ponto \(x=1\).
- Calcule a reta secante ao gráfico de \(f(x)=e^x\) passando por \((0,1)\) e \((1,e)\).













