Retas Paralelas — Definição, Condições e Exemplos
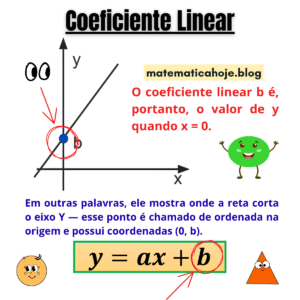
As retas paralelas são elementos fundamentais na Geometria Analítica, pois indicam duas retas que possuem a mesma direção e inclinação, mas nunca se encontram, independentemente de quanto sejam prolongadas no plano cartesiano.
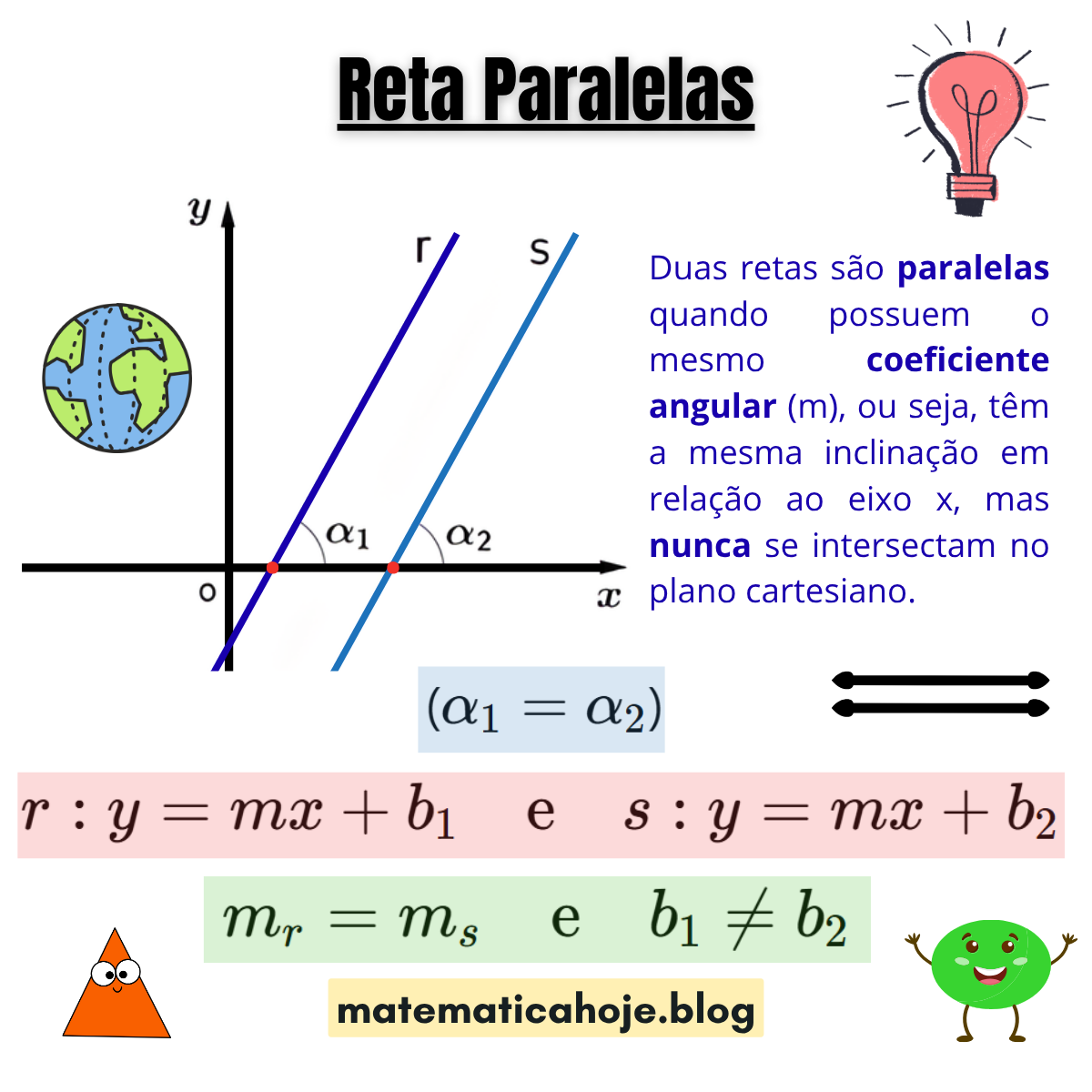
📘 O que são Retas Paralelas
Duas retas são paralelas quando apresentam o mesmo coeficiente angular (m), o que significa que têm a mesma inclinação em relação ao eixo x. Por isso, elas são **equidistantes** em todos os pontos e nunca se interceptam.
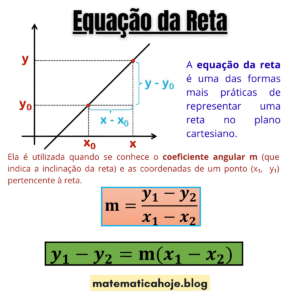
Sejam as retas \( r \) e \( s \) representadas pelas seguintes equações:
Elas serão paralelas se:
Ou seja, têm o mesmo coeficiente angular, mas diferentes coeficientes lineares — o que garante que estejam na mesma direção, porém em posições distintas no plano.
🧮 Interpretação Geométrica
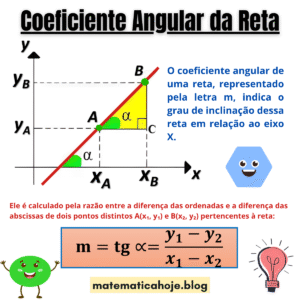
O coeficiente angular \( m \) representa o grau de inclinação da reta em relação ao eixo \(x\). Quando duas retas têm o mesmo valor de \( m \), elas formam **ângulos iguais** com o eixo \(x\), como mostrado na imagem (\( \alpha_1 = \alpha_2 \)).
📐 Exemplo 1
Exemplo: Determine se as retas \( r: y = 2x + 1 \) e \( s: y = 2x – 3 \) são paralelas.
📐 Exemplo 2
Exemplo: As retas \( y = -\frac{1}{3}x + 2 \) e \( y = -\frac{1}{3}x – 4 \) são paralelas?
📘 Domine TODAS as Fórmulas de Matemática!
Baixe o eBook Fórmulas Matemática e tenha acesso às principais fórmulas de Geometria, Álgebra, Trigonometria e muito mais — tudo organizado para revisões rápidas e eficazes!
📥 Baixar Agora — É Grátis!📚 Exercícios de Fixação
1. Determine se as retas \( y = 5x + 2 \) e \( y = 5x – 7 \) são paralelas.
2. Verifique se \( r: y = 3x + 1 \) e \( s: y = -3x + 1 \) são paralelas.