Questão de geometria com triângulo retângulo, potência de um ponto e Teorema de Tales.
Enunciado
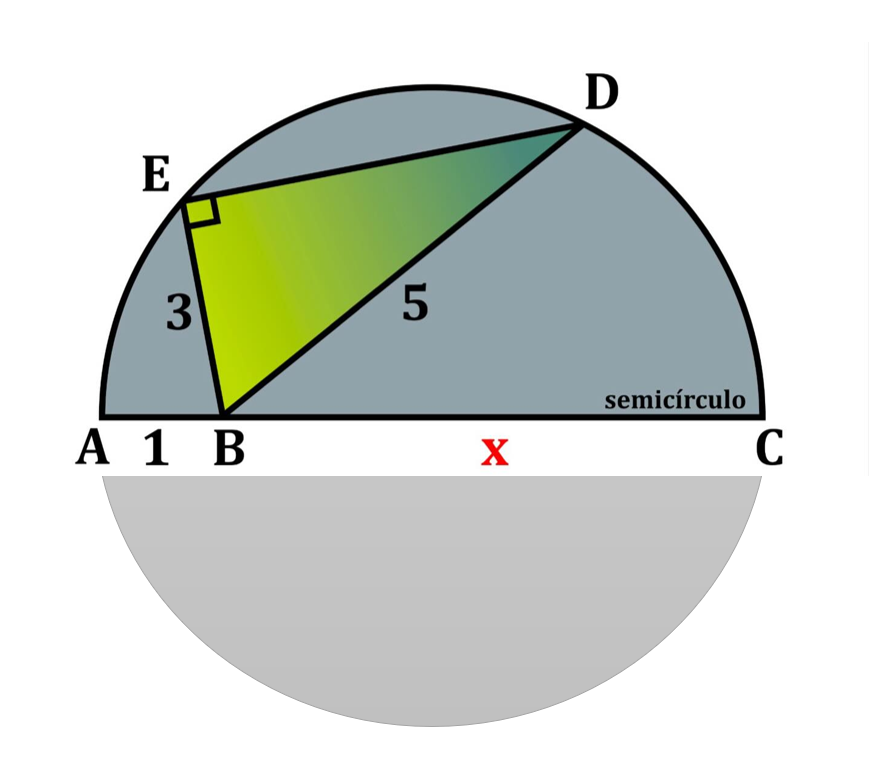
No semicírculo de diâmetro \(AC\), o ponto \(B\) pertence ao diâmetro e satisfaz \(AB=1\). Os pontos \(E\) e \(D\) pertencem ao arco do semicírculo. Sabe-se que \(BE=3\), \(BD=5\) e o ângulo \(\angle BED\) é reto. Determine o valor de \(x = BC\).
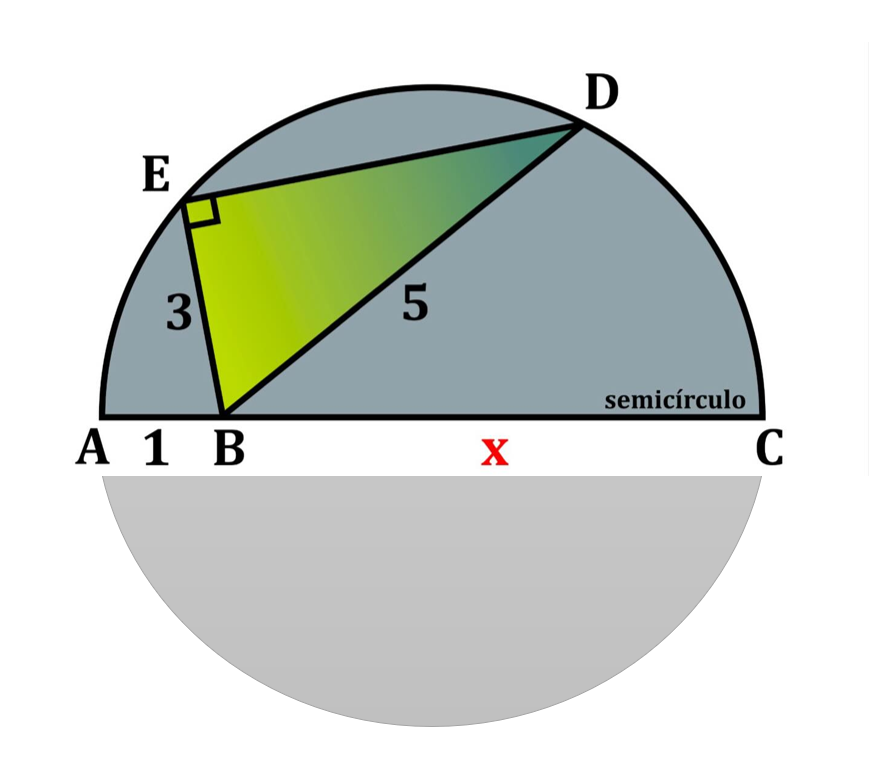
1) Encontrar \(ED\) no triângulo retângulo \(EBD\)
Como \(\angle BED = 90^\circ\), o triângulo \(EBD\) é retângulo em \(E\). Aplicando Pitágoras:
2) Construção do ponto \(P\): prolongar \(BE\) até a circunferência
Prolongue o segmento \(BE\) além de \(E\) até ele voltar a encontrar a circunferência do círculo (o círculo completo do qual o semicírculo faz parte). Chame esse segundo ponto de interseção de \(P\). Defina:
Agora use a potência do ponto \(B\): a secante \(BAC\) corta a circunferência em \(A\) e \(C\), e a secante \(BEP\) corta em \(E\) e \(P\).
3) Mostrar que \(DP\) é um diâmetro
Note que \(P\) está na mesma reta de \(B\) e \(E\). Logo, \(EP\) é o prolongamento de \(EB\). Como \(ED \perp EB\), então também temos:
Pelo Teorema de Tales, se um ângulo inscrito mede \(90^\circ\), então ele subtende um diâmetro. Portanto, \(DP\) é um diâmetro do círculo.
O diâmetro do círculo também é \(AC\). Assim:
4) Pitágoras no triângulo retângulo \(EDP\) e cálculo de \(x\)
No triângulo retângulo \(EDP\) (reto em \(E\)):
Substituindo \(DP=1+3y\), \(ED=4\) e \(EP=3+y\):
Como \(x = 3y\), concluímos:
Resposta: \(\boxed{x = 3\sqrt3}\).






















