Sequências — Guia Completo

Estrutura-base para um artigo didático: definição, formas de representação, PA, PG, propriedades e aplicações, com exercícios interativos.

📘 Mapas Mentais ➕ PA ✖ PG

Definição e ideias iniciais

Sequência é uma função de domínio nos naturais $ \mathbb{N} $ (ou em um subconjunto), escrita $ (a_n) $, onde cada termo tem posição $n$. Trabalhe a noção de padrão e de regra.

\[ \text{Explícita: } a_n=f(n)\qquad\text{Recorrente: } a_n=g(a_{n-1},a_{n-2},\dots) \]

Diagrama ilustrando sequência como função em N — Sequências.

Exemplo simples: $a_n=2n+1$ gera $1,3,5,7,\dots$. Conecte com função afim e com gráficos de pontos $(n,a_n)$.

Representações e formas de definição

Listas, tabelas e gráficos de pontos

Apresente a sequência como lista, como tabela $n \times a_n$ e como nuvem de pontos no plano (discreto).

Explícita x Recorrente

Mostre equivalências simples, como transformar $a_n=a_{n-1}+3,\ a_1=2$ em $a_n=3n-1$.

Sequências especiais

Fibonacci: $F_n=F_{n-1}+F_{n-2}$, $F_1=F_2=1$.
Sequências definidas por partes, sinais alternantes etc.

Exercícios do tópico

Ex. 1 Complete a regra explícita de $2,5,8,11,\dots$.

Ver solução

$a_n=2+3(n-1)=3n-1$.

Ex. 2 Dada $a_n=4\cdot 2^{n-1}$, escreva os 5 primeiros termos.

Ver solução

$4,8,16,32,64$.

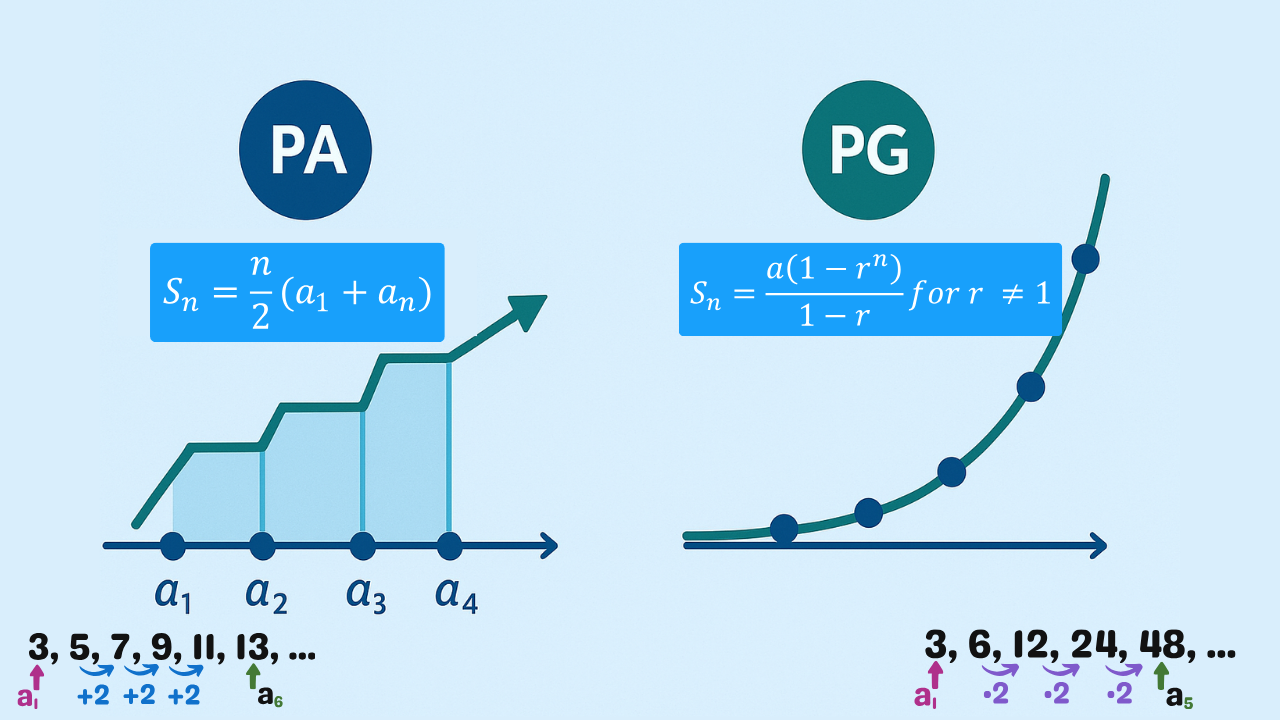
Progressão Aritmética (PA)

Sequência com variação aditiva constante $r$. Termo geral e soma:

\[ a_n=a_1+(n-1)r,\qquad S_n=\frac{n(a_1+a_n)}{2}=\frac{n}{2}[\,2a_1+(n-1)r\,]. \]

Link útil: Progressão Aritmética (PA).

Ex. 1 Encontre $a_{20}$ para $a_1=7,\ r=5$.

Ver solução

$a_{20}=7+19\cdot5=102.$

Ex. 2 Calcule $S_{12}$ para $a_1=4,\ r=3$.

Ver solução

$a_{12}=37\Rightarrow S_{12}=12(4+37)/2=246.$

Progressão Geométrica (PG)

Sequência com variação multiplicativa constante $q$. Termo geral, soma finita e soma infinita ($|q|<1$):

\[ a_n=a_1q^{n-1},\quad S_n=a_1\frac{q^n-1}{q-1}=\frac{a_1(1-q^n)}{1-q},\quad S_\infty=\frac{a_1}{1-q}\ (|q|<1). \]

Link útil: Progressão Geométrica (PG).

Ex. 1 $a_1=5,\ q=2$. Encontre $a_{12}$.

Ver solução

$a_{12}=5\cdot 2^{11}=10240.$

Ex. 2 $a_1=3,\ q=\tfrac12$. Calcule $S_\infty$.

Ver solução

$S_\infty=3/(1-1/2)=6.$

Propriedades globais de sequências

Monotonicidade: crescente, decrescente, alternante (em PG com $q<0$).
Limitação: superior/inferior (ex.: PG com \(0
Tendência (limite informal): aproximar-se de 0 em PG com $|q|<1$; crescer sem limites em $q>1$.

Ex. 1 Classifique $9,6,4,\tfrac{8}{3},\dots$.

Ver solução

PG decrescente com $q=2/3$.

Ex. 2 Uma PA com $r=0$ é limitada?

Ver solução

Sim, é constante: todos os termos iguais a $a_1$.

Modelagem e aplicações

PA: parcelamentos com acréscimo fixo, produção mensal linear, indicadores com variação constante.
PG: juros compostos, depreciação, crescimento populacional, atenuação de sinais.
Sequências especiais: Fibonacci em contagem de combinações e natureza.

Ex. (juros compostos) R$ 1.000 a 5% a.m. por 12 meses.

Ver solução

$M=1000\cdot 1{,}05^{12}\approx 1795{,}86$.