Sim, existe uma forma mais simples de simplificar a expressão
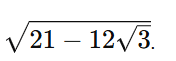
Essa expressão é um tipo específico de número conhecido como uma “forma quadrática conjugada”, que pode ser expressa como:
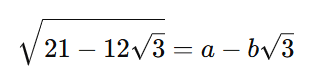
Para encontrar ( a ) e ( b ), podemos usar uma abordagem direta sem expandir tanto os cálculos.
Passo 1: Supor que
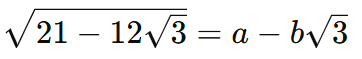
Elevando ambos os lados ao quadrado, temos:
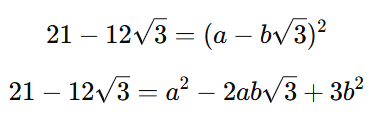
Agora, igualamos os coeficientes dos termos com e sem √3:
- Para os termos sem √3:
a2 + 3b2 = 21 - Para os termos com √3:
-2ab = -12
ab = 6
Passo 2: Resolver o sistema de equações
Agora temos o sistema:
a2 + 3b2 = 21
ab = 6
Vamos tentar valores inteiros para ( a ) e ( b ) que satisfaçam essas equações.
- Escolha ( a = 3 ):
- Se ( a = 3 ), então ( b = 6/3 = 2 ).
- Verifique se esses valores satisfazem a primeira equação:
a2 + 3b2 = 32 + 3 ⋅ 22 = 9 + 3 ⋅ 4 = 9 + 12 = 21
Esses valores satisfazem ambas as equações, então:
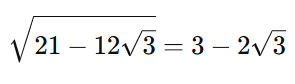
Resumo
A simplificação de
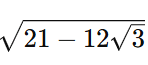
é:
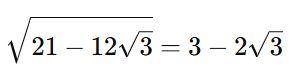
Essa abordagem evita os passos mais longos e torna a simplificação mais direta.













