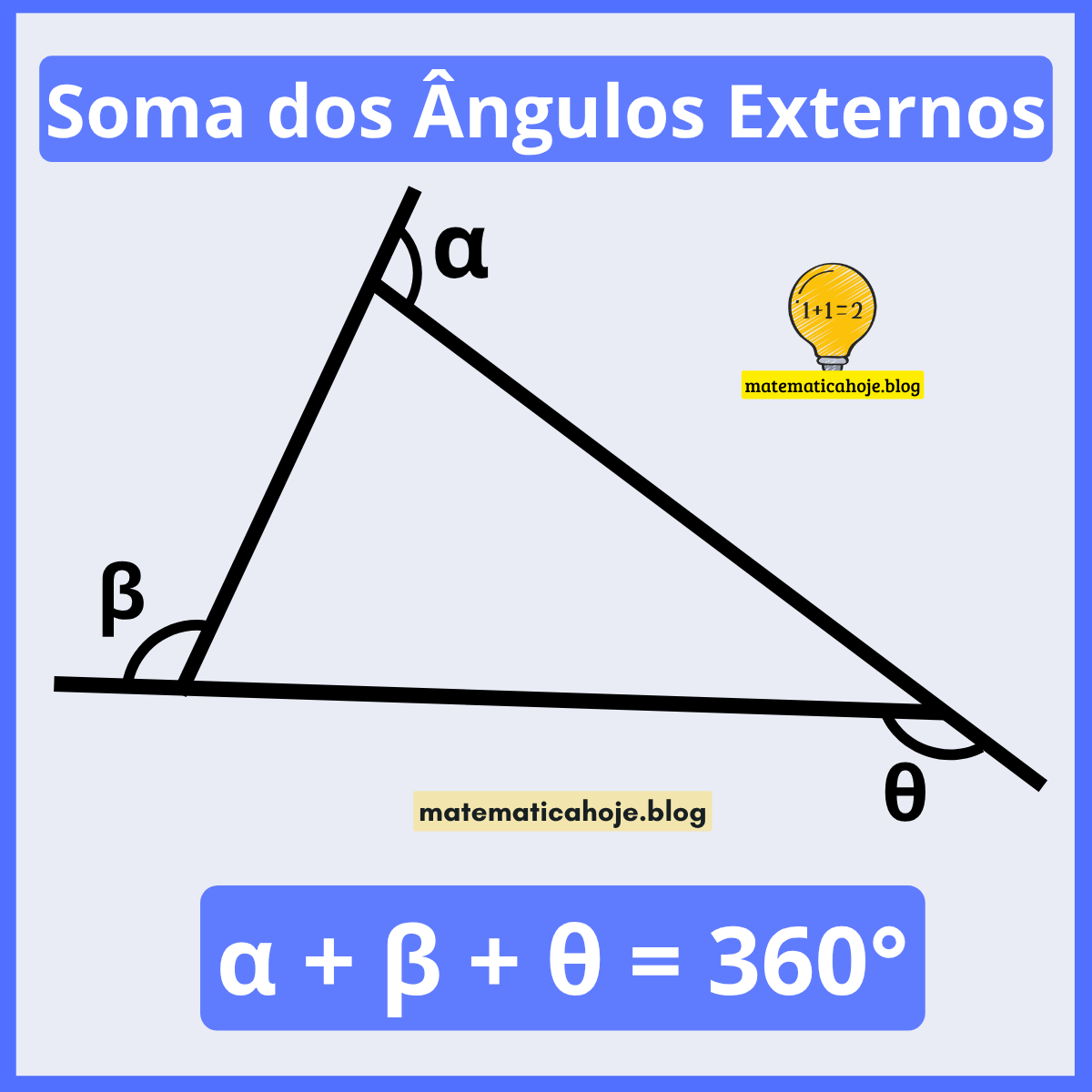
Soma dos Ângulos Externos do Triângulo

Soma dos Ângulos Externos do Triângulo (α + β + θ = 360°): teoria, exemplos e exercícios

Soma dos Ângulos Externos do Triângulo — \( \alpha + \beta + \theta = 360^\circ \)

Veja por que os três ângulos externos (um em cada vértice) somam 360°, como relacioná-los com os ângulos internos e como aplicar em questões.

Ideia-chave: escolhendo um ângulo externo em cada vértice do triângulo (o que é suplementar ao interno adjacente), a soma deles é sempre 360°.

Regra principal: \( \alpha_{\text{ext}} + \beta_{\text{ext}} + \theta_{\text{ext}} = 360^\circ \)

Como cada externo é suplementar ao interno: \( \alpha_{\text{ext}} = 180^\circ – \alpha_{\text{int}} \) (e assim por diante).

Triângulo com ângulos externos α, β e θ indicando que a soma é 360°
Imagem: matematicaoje.blog — soma dos ângulos externos

Por que os ângulos externos somam 360°?

Os três ângulos externos, um em cada vértice, formam um giro completo em torno do triângulo. Outra forma de ver é pela relação com os internos:

\(\alpha_e = 180^\circ – \alpha_i\) \(\beta_e = 180^\circ – \beta_i\) \(\theta_e = 180^\circ – \theta_i\) \(\alpha_e+\beta_e+\theta_e = 3\cdot 180^\circ – (\alpha_i+\beta_i+\theta_i)\) \(\alpha_e+\beta_e+\theta_e = 540^\circ – 180^\circ\) \(\alpha_e+\beta_e+\theta_e = 360^\circ\)

Observe como a soma dos internos \(=180^\circ\) entra naturalmente na dedução.

Mapas Mentais de Matemática

Esquematize triângulos, polígonos, ângulos, regras de sinais (adição e subtração de inteiros, multiplicação e divisão com sinais — “jogo de sinais”) e muito mais.

Exemplos resolvidos (passo a passo)

Exemplo 1 — Somando externos diretamente

No triângulo, os ângulos externos medem \(120^\circ\), \(95^\circ\) e \(x\). Calcule \(x\).

\(120^\circ + 95^\circ + x = 360^\circ\) \(215^\circ + x = 360^\circ\) \(x = 360^\circ – 215^\circ\) \(x = 145^\circ\)

Exemplo 2 — Usando a relação com ângulos internos

Em um triângulo, os ângulos internos são \( \alpha_i=50^\circ \), \( \beta_i=61^\circ \) e \( \theta_i=69^\circ \). Encontre a soma dos externos correspondentes.

\(\alpha_e = 180^\circ – 50^\circ = 130^\circ\) \(\beta_e = 180^\circ – 61^\circ = 119^\circ\) \(\theta_e = 180^\circ – 69^\circ = 111^\circ\) \(\alpha_e + \beta_e + \theta_e = 130^\circ + 119^\circ + 111^\circ\) \(= 360^\circ\)

Exemplo 3 — Com incógnitas algébricas

Os ângulos externos de um triângulo são \( (x+20)^\circ \), \( (2x-10)^\circ \) e \( (3x-50)^\circ \). Encontre \(x\) e os ângulos.

\((x+20) + (2x-10) + (3x-50) = 360\) \(6x – 40 = 360\) \(6x = 360 + 40\) \(6x = 400\) \(x = \dfrac{400}{6}\) \(x \approx 66{,}67\) Ângulos: \(86{,}67^\circ\), \(123{,}33^\circ\), \(150^\circ\)

eBook Gratuito de Fórmulas Matemáticas

Inclui quadro de ângulos, polígonos, potência e radiciação, além de revisão de operações com números inteiros (regras de sinais: adição, subtração, multiplicação e divisão).

Exercícios propostos (com toggle)

Resolva e depois abra o abre/fecha para conferir. Mantenha as contas uma abaixo da outra após o “=” para melhor leitura em celulares.

1) Discursiva — Sinalização urbana

Uma placa triangular é instalada formando com o chão um ângulo externo de \(112^\circ\) em um vértice e \(x\) no segundo. No terceiro vértice, o externo mede \(128^\circ\). Calcule \(x\).

Ver solução
\(112^\circ + x + 128^\circ = 360^\circ\) \(x + 240^\circ = 360^\circ\) \(x = 360^\circ – 240^\circ\) \(x = 120^\circ\)

2) Múltipla escolha — Projeto de telhado

Os ângulos externos são \(x\), \(2x\) e \(3x\). O valor de \(x\) é:

  1. \(30^\circ\)
  2. \(45^\circ\)
  3. \(60^\circ\)
  4. \(90^\circ\)
Mostrar alternativa correta
\(x + 2x + 3x = 360^\circ\) \(6x = 360^\circ\) \(x = \dfrac{360^\circ}{6}\) \(x = 60^\circ\)

Resposta: Letra C.

3) Discursiva — Relação com o interno

Em um vértice, o interno mede \(38^\circ\). Qual é o ângulo externo correspondente? Em seguida, suponha que os outros dois externos sejam \(x\) e \(y\) e calcule \(x+y\).

Ver solução
Externo \(= 180^\circ – 38^\circ\) Externo \(= 142^\circ\) Soma dos três externos \(= 360^\circ\) Logo, \(x + y = 360^\circ – 142^\circ\) \(x + y = 218^\circ\)

4) Múltipla escolha — Expressões algébricas

Se os externos são \( (x+15)^\circ \), \( (2x+25)^\circ \) e \( (3x-40)^\circ \), então \(x\) vale:

  1. 40
  2. 45
  3. 50
  4. 55
Mostrar resposta
\((x+15) + (2x+25) + (3x-40) = 360\) \(6x = 360\) \(x = \dfrac{360}{6}\) \(x = 60\)

Gabarito: nenhuma das alternativas (boa checagem de atenção). Ajuste para incluir 60 nas opções.

5) Discursiva — Revisão com inteiros e “jogo de sinais”

Para treinar aritmética: calcule \(+360 – [ (+95) + (-120) ]\), aplicando as regras de sinais de operações com números inteiros.

Ver solução (inteiros)
\(+360 – ( +95 + (-120) )\) \(= +360 – ( -25 )\) \(= +360 + 25\) \(= 385\)

Links úteis & produtos do blog

ENEM Matemática — trilha de estudos, listas e simulados 10 eBooks de Matemática — pacote completo para revisão Banco de Questões de Matemática — centenas de itens editáveis Mapas Mentais de Matemática — revisão visual rápida eBook Gratuito de Fórmulas Matemáticas — baixe agora

Artigos relacionados

Conclusão

Escolhendo um ângulo externo em cada vértice, sua soma é sempre 360°. Essa propriedade facilita contas, permite montar equações simples e aparece com frequência em provas (inclusive no ENEM). Consolide a ideia praticando várias configurações e relacionando com os ângulos internos.

Convite: baixe o eBook gratuito de Fórmulas e acompanhe nossas novidades e listas no canal do WhatsApp via página ENEM Matemática.

Conteúdo otimizado para SEO: usamos variações como “operações com números inteiros”, “regras de sinais”, “adição e subtração de inteiros”, “multiplicação e divisão com sinais”, “matemática básica” e “jogo de sinais” para conectar revisão aritmética às resoluções de geometria.

Relacionadas

Triângulo Escaleno

Ângulos Complementares

Teorema do Ângulo Externo

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube