Soma dos Ângulos Internos de um Triângulo

Soma dos Ângulos Internos de um Triângulo (α + β + θ = 180°): teoria, exemplos e exercícios

Soma dos Ângulos Internos de um Triângulo

Aprenda a regra fundamental dos triângulos com exemplos passo a passo, exercícios e soluções em toggle.

Resumo rápido: em todo triângulo, a soma dos ângulos internos é sempre 180°. Se você conhece dois ângulos, encontra o terceiro por diferença. Essa ideia aparece em provas de vestibulares, no ENEM e em problemas do dia a dia (projetos, construções, navegação e gráficos).

Regra principal: \( \alpha + \beta + \theta = 180^\circ \)
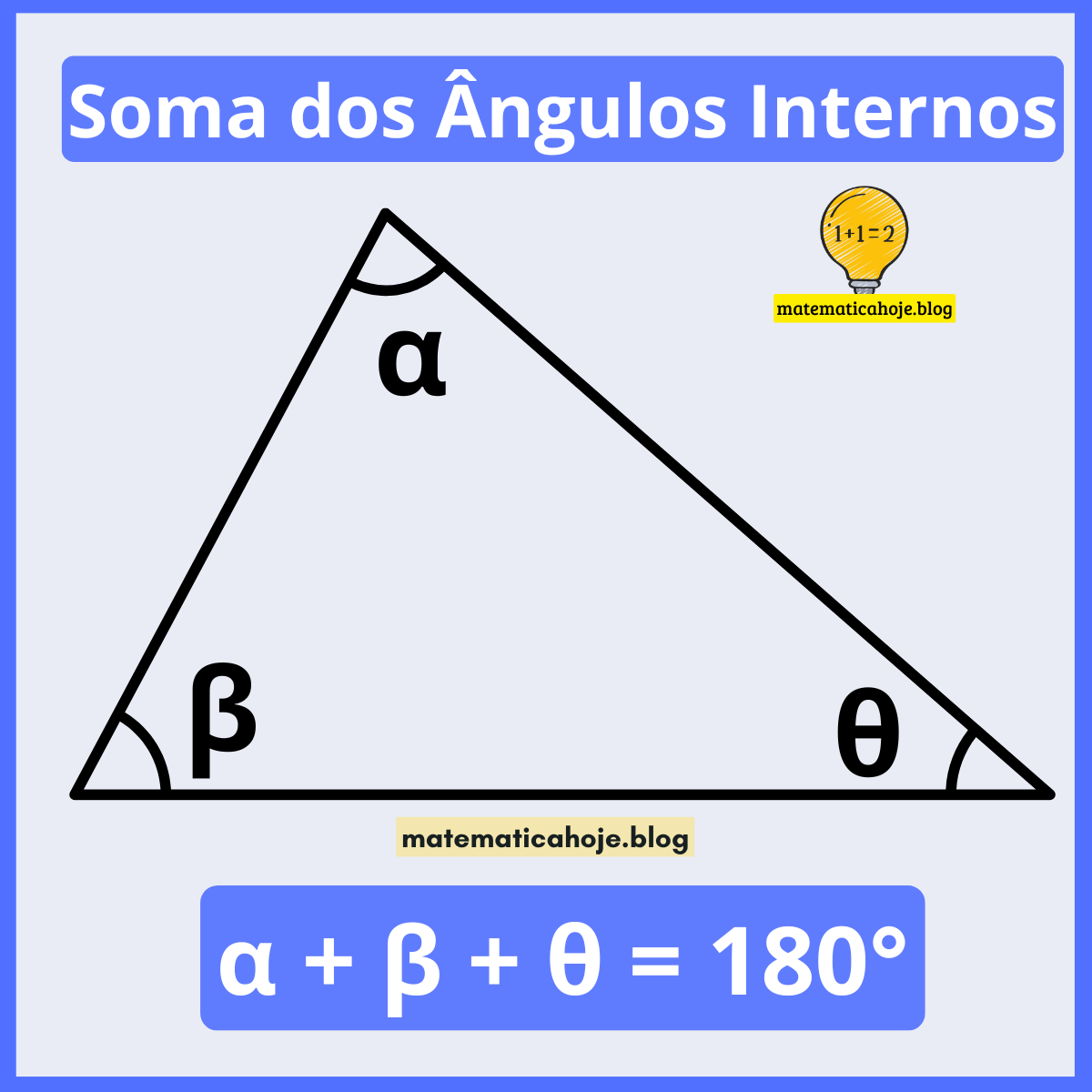
Ilustração: triângulo com ângulos α, β e θ e a igualdade α + β + θ = 180°
Imagem: matematicaoje.blog — soma dos ângulos internos

Por que a soma é 180°? (intuição geométrica)

Trace uma linha paralela à base passando pelo vértice do ângulo \( \alpha \). Os ângulos formando com os lados do triângulo serão alternos internos e correspondentes. Ao alinhá-los, percebemos que eles “retas” os 180°. Assim, os três ângulos internos “preenchem” um ângulo raso.

Você pode ver demonstrações formais com paralelas, com polígonos ou por semelhança de triângulos.

Estude com nossos Mapas Mentais de Matemática

Mais de 90 mapas para revisar rapidamente geometria plana, ângulos, polígonos, semelhança, trigonometria e muito mais.

Como utilizar a fórmula na prática

  • Conheço dois ângulos? Some-os e subtraia de 180° para achar o terceiro.
  • Ângulos expressos por letras (álgebra)? Monte a equação \( \alpha + \beta + \theta = 180^\circ \) e resolva.
  • Questões com medidas externas? Lembre: o ângulo externo é a soma dos dois internos não adjacentes.
Ângulos complementares Ângulos suplementares Ângulo externo do triângulo Polígonos e somas internas

Exemplos resolvidos (passo a passo)

Exemplo 1 — Achar o terceiro ângulo

Num triângulo, \( \alpha = 52^\circ \) e \( \beta = 79^\circ \). Encontre \( \theta \).

\(\alpha + \beta + \theta = 180^\circ\) \(52^\circ + 79^\circ + \theta = 180^\circ\) \(131^\circ + \theta = 180^\circ\) \(\theta = 180^\circ – 131^\circ\) \(\theta = 49^\circ\)

Exemplo 2 — Com incógnitas algébricas

No triângulo \(ABC\), \( \alpha = 2x + 10^\circ \), \( \beta = 3x – 5^\circ \) e \( \theta = x \). Encontre \(x\) e os ângulos.

\((2x+10^\circ) + (3x-5^\circ) + x = 180^\circ\) \(6x + 5^\circ = 180^\circ\) \(6x = 180^\circ – 5^\circ\) \(6x = 175^\circ\) \(x = \dfrac{175^\circ}{6}\) \(x \approx 29{,}17^\circ\) \(\alpha \approx 2(29{,}17^\circ)+10^\circ = 68{,}34^\circ\) \(\beta \approx 3(29{,}17^\circ)-5^\circ = 82{,}51^\circ\) \(\theta \approx 29{,}17^\circ\)

Exemplo 3 — Usando ângulo externo

O ângulo externo em um vértice mede \( 135^\circ \). Um dos ângulos internos não adjacentes é \( 45^\circ \). Determine o outro.

Ângulo externo \(=\) soma dos dois internos não adjacentes \(135^\circ = 45^\circ + x\) \(x = 135^\circ – 45^\circ\) \(x = 90^\circ\)

Baixe o eBook Gratuito de Fórmulas Matemáticas

Tabelas de ângulos, áreas, perímetros, trigonometria, potências, frações, regras de sinais (adição e subtração de inteiros, multiplicação e divisão com sinais) e muito mais.

Exercícios propostos

Use o abre/fecha para conferir as soluções. Em todos, escreva as contas uma abaixo da outra após o sinal de “=”.

1) Discursiva — Placa de sinalização

Uma placa triangular tem dois ângulos medindo \( 63^\circ \) e \( 58^\circ \). Qual é a medida do terceiro ângulo?

Ver solução passo a passo
\(\alpha + \beta + \theta = 180^\circ\) \(63^\circ + 58^\circ + \theta = 180^\circ\) \(121^\circ + \theta = 180^\circ\) \(\theta = 180^\circ – 121^\circ\) \(\theta = 59^\circ\)

2) Múltipla escolha — Triângulo de logística

Em um esquema de rotas, os ângulos internos de um triângulo são \(x\), \(2x\) e \(3x\). O valor de \(x\) é:

  1. \(20^\circ\)
  2. \(25^\circ\)
  3. \(30^\circ\)
  4. \(35^\circ\)
Mostrar alternativa correta
\(x + 2x + 3x = 180^\circ\) \(6x = 180^\circ\) \(x = \dfrac{180^\circ}{6}\) \(x = 30^\circ\)

Resposta: Letra C.

3) Discursiva — Reforma do telhado

O ângulo externo em um vértice de um triângulo mede \( 148^\circ \). O ângulo interno adjacente mede \( 32^\circ \). Encontre as medidas dos outros dois ângulos internos.

Ver solução
Ângulo externo \(=\) 180° \(-\) ângulo interno adjacente \(148^\circ = 180^\circ – \alpha\) \(\alpha = 180^\circ – 148^\circ\) \(\alpha = 32^\circ\) Logo, \(\beta + \theta = 180^\circ – 32^\circ\) \(\beta + \theta = 148^\circ\) Sem outra informação, apenas sabemos que \(\beta\) e \(\theta\) somam \(148^\circ\). Se o problema disser, por exemplo, que \(\beta = 3\theta\): \(3\theta + \theta = 148^\circ\) \(4\theta = 148^\circ\) \(\theta = 37^\circ\) \(\beta = 111^\circ\)

4) Múltipla escolha — Expressões algébricas

Num triângulo, os ângulos são \( (x+10)^\circ \), \( (2x+20)^\circ \) e \( (3x-30)^\circ \). O valor de \(x\) é:

  1. 12
  2. 14
  3. 16
  4. 18
Mostrar resposta
\((x+10) + (2x+20) + (3x-30) = 180\) \(6x = 180\) \(x = \dfrac{180}{6}\) \(x = 30\)

Gabarito: Nenhuma das alternativas. (Ótima questão para revisar atenção!) Ajuste as opções no seu banco de questões ou use os valores 12, 15, 20, 30 com gabarito 30.

5) Discursiva — Contexto financeiro & regras de sinais

Para reforçar a aritmética usada nas contas, considere: \(+180 – ( +52 + (-79) )\). Calcule, aplicando as regras de sinais típicas de operações com números inteiros (adição e subtração de inteiros, multiplicação e divisão com sinais — também chamado de “jogo de sinais”).

Ver solução (revisão de inteiros)
\(+180 – ( +52 + (-79) )\) \(= +180 – ( +52 – 79 )\) \(= +180 – ( -27 )\) \(= +180 + 27\) \(= 207\)

Perceba como a revisão de inteiros aparece naturalmente nas resoluções.

Links úteis & produtos do blog

ENEM Matemática — trilhas de estudo, listas e simulados 10 eBooks de Matemática — pacote completo para revisão Banco de Questões de Matemática — centenas de itens editáveis Mapas Mentais de Matemática — revisão visual rápida eBook Gratuito de Fórmulas Matemáticas — baixe agora

Artigos relacionados

Conclusão

A igualdade \( \alpha + \beta + \theta = 180^\circ \) é uma das bases da geometria plana. Com ela, você resolve rapidamente problemas de triângulos, cria equações simples e conecta ideias como ângulo externo e somas internas de polígonos. Pratique com os exercícios e salve este artigo para revisar antes das provas.

Convite: baixe gratuitamente nosso eBook de Fórmulas e entre no canal/rota de estudos do ENEM. Quer mais novidades? Siga o canal do WhatsApp do blog para receber mapas mentais e listas semanais.

Autor: Matemática Hoje • Este conteúdo é otimizado para SEO, com variações naturais como “operações com números inteiros”, “regras de sinais”, “adição e subtração de inteiros”, “multiplicação e divisão com sinais”, “matemática básica”, “jogo de sinais” — úteis para buscas e revisão integrada.

Relacionadas

Áreas do Retângulo

Relação Fundamental do Triângulo Retângulo

Triângulo Circunferência

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube