Taxa de Variação da Função Afim
A taxa de variação mede “o quanto \(y\) muda quando \(x\) varia”. Em funções afins \(f(x)=ax+b\), essa taxa é constante e coincide com o coeficiente angular \(a\). Tema direto e recorrente no ENEM e no nosso Banco de Questões.
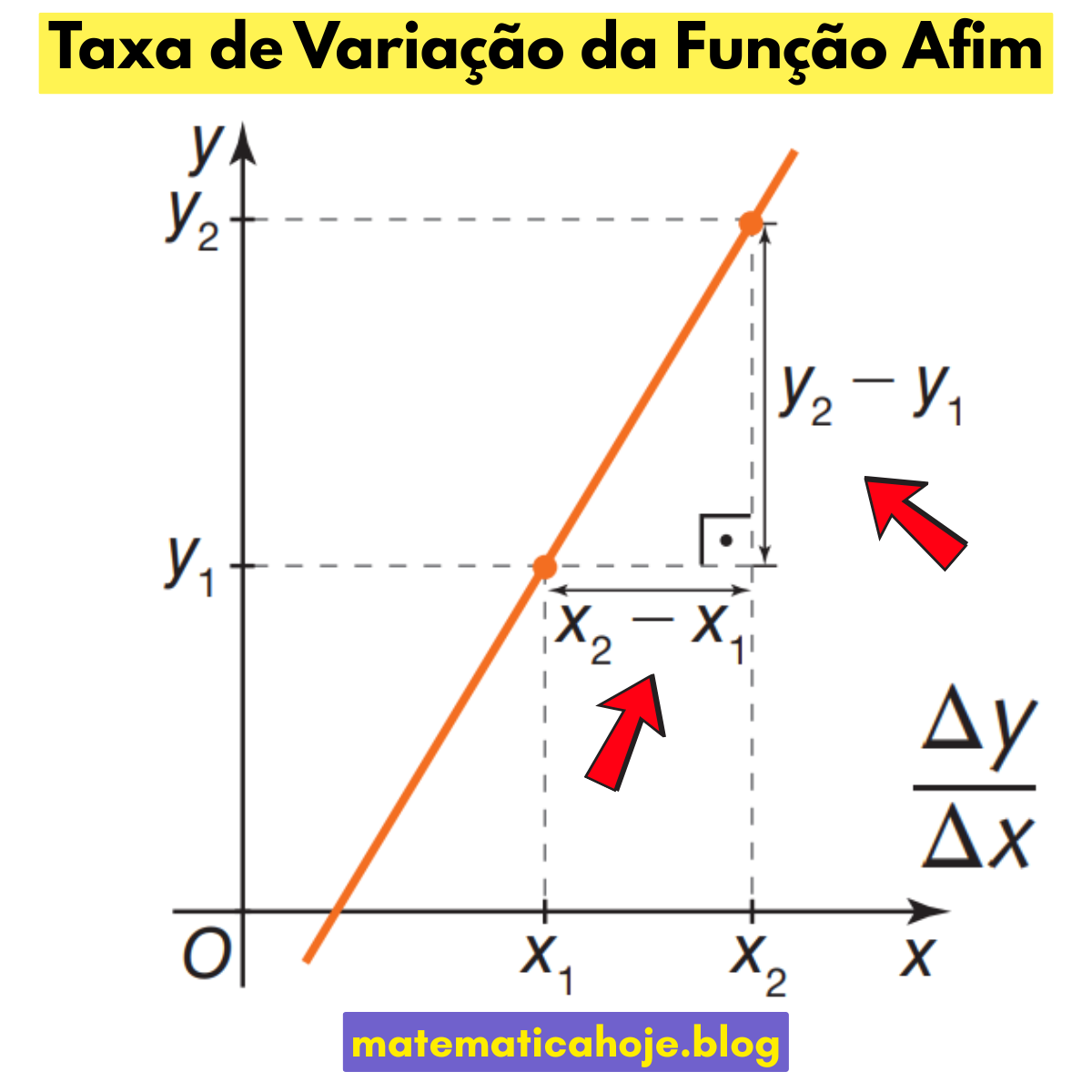
Definição (média) e ligação com a inclinação
Para \(f(x)=ax+b\):
Logo, a taxa de variação é constante e igual a \(a\) (a inclinação da reta).
Leitura no gráfico e interpretação física
- No gráfico, \(\dfrac{\Delta y}{\Delta x}\) é a “subida” sobre o “avanço” entre dois pontos.
- Em aplicações: se \(y\) é distância e \(x\) é tempo, \(\dfrac{\Delta y}{\Delta x}\) é a velocidade média. Se \(y\) é custo e \(x\) é quantidade, é o custo marginal médio, etc.
- Sinal: \(a>0\) ⇒ taxa positiva (variável cresce); \(a<0\) ⇒ taxa negativa (decresce).
- Unidades: \([\Delta y]/[\Delta x]\) (ex.: km/h, R$/unidade).
📘 Dica rápida
Reforce as fórmulas de taxas, funções e gráficos com o eBook Fórmulas Matemática.
Baixar eBook de FórmulasExemplos resolvidos
Exemplo 1 — Encontrar \(a\) a partir de dois pontos. O gráfico de \(f(x)=ax+b\) passa por \(A(1,2)\) e \(B(4,11)\). Calcule a taxa de variação e a lei da função.
Ver solução
\(\dfrac{\Delta y}{\Delta x}=\dfrac{11-2}{4-1}=\dfrac{9}{3}=3\Rightarrow a=3\).
Usando \(A\): \(2=3\cdot1+b\Rightarrow b=-1\). Logo, \(f(x)=3x-1\).
Exemplo 2 — Interpretação como velocidade. Um carro percorre 18 km aos 0,5 h e 66 km aos 2,5 h. Supondo modelo afim \(s(t)=at+b\), encontre a taxa média no intervalo e interprete.
Ver solução
\(\dfrac{\Delta s}{\Delta t}=\dfrac{66-18}{2{,}5-0{,}5}=\dfrac{48}{2}=24\ \text{km/h}\).
Velocidade média no intervalo: \(24\ \text{km/h}\). Se o movimento for afim, \(a=24\).
Exemplo 3 — Custo médio por unidade. Uma empresa modela \(C(q)=4q+150\) (R$), onde \(q\) é a quantidade produzida. Qual a taxa de variação do custo?
Ver solução
É a inclinação: \(a=4\). A cada unidade adicional, o custo cresce R$ 4,00.
Exercícios (com solução no abre/fecha)
1) Para \(f(x)=2x+5\), calcule a taxa de variação entre \(x=3\) e \(x=9\) e compare com \(a\).
Ver solução
\(\dfrac{f(9)-f(3)}{9-3}=\dfrac{(23)-(11)}{6}=\dfrac{12}{6}=2=a\).
2) A função \(g(x)=-0{,}8x+12\) descreve a temperatura \(T\) (°C) em função da altitude \(h\) (km). Interprete a taxa.
Ver solução
\(a=-0{,}8\ \text{°C/km}\): a cada 1 km de altitude, a temperatura diminui 0,8 °C.
3) A reta que liga \(P(-2,-3)\) a \(Q(6,5)\) representa uma função afim. Determine a taxa e a lei \(f(x)\).
Ver solução
\(a=\dfrac{5-(-3)}{6-(-2)}=\dfrac{8}{8}=1\). Usando \(P\): \(-3=1\cdot(-2)+b\Rightarrow b=-1\). \(f(x)=x-1\).
4) Em um serviço de streaming, o custo mensal total é \(C(h)=0{,}50h+29{,}90\), onde \(h\) são as horas assistidas. Qual a taxa e o que ela significa?
Ver solução
Taxa \(a=0{,}50\ \text{R$/h}\): cada hora adicional adiciona R$ 0,50 ao custo.
5) Uma função afim tem taxa \(-3\) e passa por \((0,7)\). Encontre sua lei e diga se é crescente ou decrescente.
Ver solução
\(a=-3\), \(b=7\) ⇒ \(f(x)=-3x+7\). Como \(a<0\), é decrescente.
Para continuar
- Revise o resumo de Funções e compare com Função Quadrática.
- Veja aplicações em gráficos e interseções de retas no blog e pratique no Banco de Questões.
- Organize sua revisão com Mapas Mentais de Matemática e materiais do Pacote com 10 eBooks.













