Hoje vamos estudar um dos resultados mais importantes da geometria: o Teorema da Bissetriz Interna. Ele aparece muito em provas do ENEM, concursos públicos e vestibulares, e costuma gerar dúvidas porque envolve segmentos e proporções — mas a verdade é que, depois que você entende a lógica, ele fica simples.
Então vamos fazer o seguinte: primeiro entendemos a ideia, depois a fórmula, e por fim resolvemos vários exemplos para treinar.
1️⃣ O que é uma bissetriz interna?
Antes de tudo, precisamos lembrar: bissetriz é o segmento que divide um ângulo em duas partes iguais.
No triângulo abaixo, o segmento $\\overline{AD}$ divide o ângulo $\\angle A$ ao meio, formando dois ângulos iguais:
$\angle BAD = \angle DAC$.
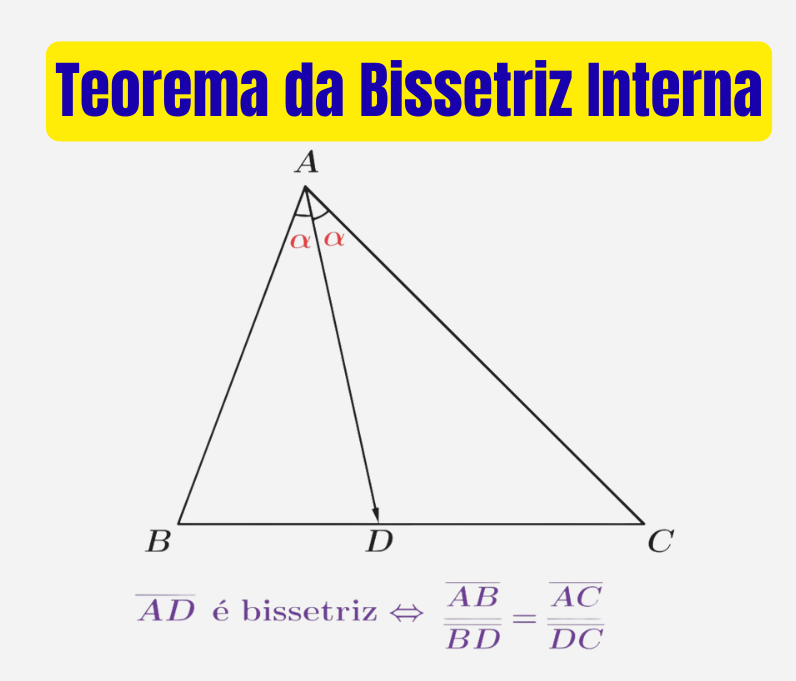
Agora vem a parte mais importante: quando essa bissetriz encontra o lado oposto, ela não divide esse lado ao meio — isso é mediana. A bissetriz divide o lado em proporção com os lados do triângulo.
2️⃣ O Enunciado do Teorema — A Fórmula
\[ \frac{AB}{AC} = \frac{BD}{DC} \]
Ou seja:
A razão entre os lados que formam o ângulo é igual à razão entre os segmentos do lado oposto.
Em forma equivalente:
\[ \overline{AD} \text{ é bissetriz } \Leftrightarrow \frac{\overline{AB}}{\overline{BD}} = \frac{\overline{AC}}{\overline{DC}}. \]
3️⃣ Por que isso funciona? (Explicação intuitiva)
Não vamos fazer uma demonstração formal aqui, mas quero que você entenda a lógica:
- Traçamos uma linha paralela à bissetriz;
- Criamos triângulos semelhantes;
- E triângulos semelhantes geram proporções iguais.
Ou seja, a bissetriz “divide o triângulo em dois triângulos parecidos”, mantendo uma proporção. Isso explica por que ela não divide o lado ao meio, mas sim de forma proporcional aos outros lados.
4️⃣ Exemplos Resolvidos
🔹 Exemplo 1: Encontrando um segmento
No triângulo $ABC$, $AD$ é bissetriz. Temos:
- $AB = 6\,\text{cm}$
- $AC = 9\,\text{cm}$
- $BD = 4\,\text{cm}$
Calcule o valor de $DC$.
\[ \frac{AB}{AC} = \frac{BD}{DC} \Rightarrow \frac{6}{9} = \frac{4}{DC} \]
\[ \begin{aligned} \frac{6}{9} &= \frac{4}{DC} \\ \frac{2}{3} &= \frac{4}{DC} \\ 2 \cdot DC &= 3 \cdot 4 \\ 2\,DC &= 12 \\ DC &= 6\,\text{cm} \end{aligned} \]
Resposta: $DC = 6\,\text{cm}$
🔹 Exemplo 2: Encontrando um lado do triângulo
No triângulo $ABC$, $AD$ é bissetriz. Sabe-se que:
- $BD = 3\,\text{cm}$
- $DC = 7\,\text{cm}$
- $AB = 10\,\text{cm}$
Calcule o valor de $AC$.
\[ \frac{AB}{AC} = \frac{BD}{DC} \Rightarrow \frac{10}{AC} = \frac{3}{7} \]
\[ \begin{aligned} 10 \cdot 7 &= 3 \cdot AC \\ 70 &= 3AC \\ AC &= \frac{70}{3} \\ AC &\approx 23{,}33\,\text{cm} \end{aligned} \]
Resposta: $AC \approx 23{,}33\,\text{cm}$
🔹 Exemplo 3: Situação do ENEM (Interpretação)
Em um triângulo $ABC$, sabe-se que $AD$ é bissetriz. Se:
- $AB = 5\,\text{cm}$
- $AC = 8\,\text{cm}$
- $BC = 13\,\text{cm}$
Determine os valores de $BD$ e $DC$.
Sabemos que:
\[ \frac{AB}{AC} = \frac{BD}{DC} \Rightarrow \frac{5}{8} = \frac{BD}{DC} \]
Além disso:
\[ BD + DC = 13 \Rightarrow DC = 13 – BD \]
Substituindo:
\[ \frac{5}{8} = \frac{BD}{13 – BD} \]
\[ \begin{aligned} 5(13 – BD) &= 8BD \\ 65 – 5BD &= 8BD \\ 65 &= 13BD \\ BD &= 5\,\text{cm} \\ DC &= 8\,\text{cm} \end{aligned} \]
Resposta: $BD = 5\,\text{cm}$ e $DC = 8\,\text{cm}$
5️⃣ Aplicações Reais
Esse teorema aparece em:
- Construções geométricas;
- Problemas de engenharia estrutural;
- Design de cálculo de divisões proporcionais;
- Divisão estratégica de áreas em arquitetura;
- E claro, em questões do ENEM e concursos.
6️⃣ Resumo do que você precisa lembrar
\[ \boxed{\frac{AB}{AC} = \frac{BD}{DC}} \]
Se houver bissetriz interna, sempre existe proporção entre os lados e os segmentos. Antes de aplicar o teorema, pergunte:
- O segmento divide o ângulo em duas partes iguais? → Se sim, pode usar.
- Os segmentos estão no lado oposto? → Sempre.
📚 Para continuar estudando
Se quiser mais exemplos, resumos e listas, acesse:













