Teorema de Pitágoras

Teorema de Pitágoras: como aplicar? Exemplos e exercícios

Teorema de Pitágoras: como aplicar? Exemplos e exercícios

Resumo: você usa o Teorema de Pitágoras sempre que precisa relacionar os lados de um triângulo retângulo. Neste guia prático, explico a ideia por trás da fórmula, mostro passo a passo como resolver questões (com os cálculos um abaixo do outro após o sinal de igualdade) e disponibilizo exercícios com solução para treinar agora.

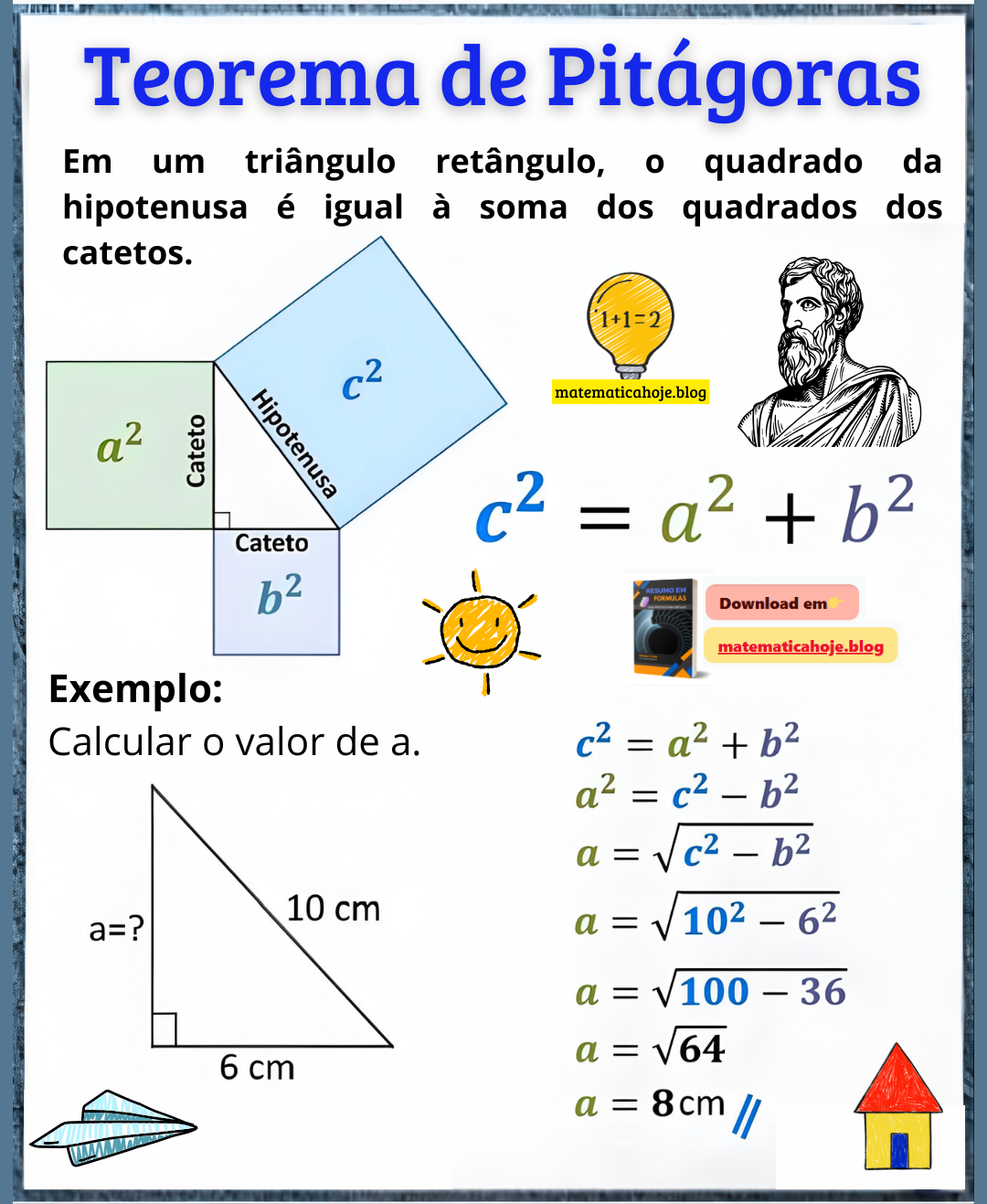
Teorema de Pitágoras - matemática hoje

O que diz o Teorema? Entenda a relação entre os lados

Em qualquer triângulo retângulo (um dos ângulos mede 90°), o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Em linguagem matemática:

\[ \begin{aligned} c^2 &= a^2 + b^2 \\ \text{onde } c &\text{ é a hipotenusa, e } a,b \text{ são os catetos.} \end{aligned} \]

Essa relação permite descobrir lados desconhecidos, checar se três medidas formam um triângulo retângulo e resolver problemas práticos de distância, escadas, diagonais de telas, pisos e muito mais.

Quando usar o Teorema? Casos práticos do dia a dia

  • Distância reta: calcular a diagonal de um retângulo (tela, piso, terreno).
  • Altura e escadas: descobrir a altura alcançada por uma escada encostada na parede.
  • Roteiro de prova: checar rapidamente se um trio \((a,b,c)\) é retângulo.
  • Coordenadas: distância entre pontos no plano cartesiano.
Dica rápida. Se você reconhece trincas famosas como \((3,4,5)\), \((5,12,13)\) e múltiplas delas, ganha tempo precioso nas questões.

Exemplos resolvidos: passo a passo, linha a linha

Exemplo 1 — Encontrando um cateto

Num triângulo retângulo, \(c=10\) cm e um cateto vale \(6\) cm. Qual é o outro cateto \(a\)?

\[ \begin{aligned} c^2 &= a^2 + b^2 \\ a^2 &= c^2 – b^2 \\ a &= \sqrt{c^2 – b^2} \\ a &= \sqrt{10^2 – 6^2} \\ a &= \sqrt{100 – 36} \\ a &= \sqrt{64} \\ a &= 8\ \text{cm} \end{aligned} \]

Exemplo 2 — Diagonal de um retângulo

Um retângulo mede \(9\) m por \(12\) m. Qual é a sua diagonal \(d\)?

\[ \begin{aligned} d^2 &= 9^2 + 12^2 \\ d^2 &= 81 + 144 \\ d^2 &= 225 \\ d &= 15\ \text{m} \end{aligned} \]

Exemplo 3 — Distância entre dois pontos

Encontre a distância entre \(A(2,3)\) e \(B(11,7)\).

\[ \begin{aligned} d^2 &= (11-2)^2 + (7-3)^2 \\ d^2 &= 9^2 + 4^2 \\ d^2 &= 81 + 16 \\ d^2 &= 97 \\ d &= \sqrt{97} \end{aligned} \]
Mapas Mentais de Matemática: revise Pitágoras com esquemas visuais e ative sua memória.
Abrir Mapas Mentais

Guia rápido: fórmula, teste retângulo e truques

\[ \begin{aligned} \text{Fórmula principal: } & c^2 = a^2 + b^2 \\ \text{Cateto: } & a = \sqrt{c^2 – b^2} \\ \text{Verificar trio: } & a^2 + b^2 \stackrel{?}{=} c^2 \end{aligned} \]

Pro tip Multiplicou um trio conhecido por um número \(k\)? O resultado também é retângulo. Ex.: \((3,4,5)\) → \((6,8,10)\).

Lista de exercícios com solução (abre/fecha)

1) Hipotenusa de triângulo retângulo

Um triângulo retângulo tem catetos de \(7\) cm e \(24\) cm. Calcule a hipotenusa.

👀 Mostrar solução
\[ \begin{aligned} c^2 &= 7^2 + 24^2 \\ c^2 &= 49 + 576 \\ c^2 &= 625 \\ c &= 25\ \text{cm} \end{aligned} \]

2) Cateto desconhecido

Na figura, \(c=26\) m e um cateto é \(10\) m. Determine o outro cateto.

👀 Mostrar solução
\[ \begin{aligned} a^2 &= c^2 – b^2 \\ a^2 &= 26^2 – 10^2 \\ a^2 &= 676 – 100 \\ a^2 &= 576 \\ a &= 24\ \text{m} \end{aligned} \]

3) Diagonal de TV

Uma TV tem 48 cm de altura e 64 cm de largura. Qual a diagonal (em cm)?

👀 Mostrar solução
\[ \begin{aligned} d^2 &= 48^2 + 64^2 \\ d^2 &= 2304 + 4096 \\ d^2 &= 6400 \\ d &= 80\ \text{cm} \end{aligned} \]

4) Distância no plano

Determine a distância entre \(P(-5,2)\) e \(Q(7,-4)\).

👀 Mostrar solução
\[ \begin{aligned} d^2 &= (7-(-5))^2 + (-4-2)^2 \\ d^2 &= 12^2 + (-6)^2 \\ d^2 &= 144 + 36 \\ d^2 &= 180 \\ d &= 6\sqrt{5} \end{aligned} \]

5) Escada encostada

Uma escada de 5 m alcança uma janela a 4 m do chão. A base da escada fica a que distância da parede?

👀 Mostrar solução
\[ \begin{aligned} b^2 &= c^2 – a^2 \\ b^2 &= 5^2 – 4^2 \\ b^2 &= 25 – 16 \\ b^2 &= 9 \\ b &= 3\ \text{m} \end{aligned} \]

6) Quadrado e diagonal

Um quadrado tem lado \(x=11\) cm. Calcule a diagonal.

👀 Mostrar solução
\[ \begin{aligned} d^2 &= x^2 + x^2 \\ d^2 &= 2x^2 \\ d &= x\sqrt{2} \\ d &= 11\sqrt{2}\ \text{cm} \end{aligned} \]

7) Trinca pitagórica

Mostre que \((9,12,15)\) forma um triângulo retângulo.

👀 Mostrar solução
\[ \begin{aligned} 9^2 + 12^2 &= 81 + 144 \\ &= 225 \\ &= 15^2 \\ \text{Logo, } & \text{é triângulo retângulo.} \end{aligned} \]

8) Terreno retangular

Um terreno mede \(30\) m por \(40\) m. Um cano passa na diagonal. Qual seu comprimento?

👀 Mostrar solução
\[ \begin{aligned} d^2 &= 30^2 + 40^2 \\ d^2 &= 900 + 1600 \\ d^2 &= 2500 \\ d &= 50\ \text{m} \end{aligned} \]
Precisa das fórmulas na mão? Baixe gratuitamente nosso Formulário de Fórmulas Matemáticas e acelere seus estudos.
Baixar grátis

Conclusões e próximos passos de estudo

O Teorema de Pitágoras é um atalho poderoso para problemas de distância e diagonais. Domine a fórmula, reconheça trincas pitagóricas e treine a passagem do enunciado para o desenho. Para reforçar, resolva os exercícios desta página e explore nosso Banco de Questões. Se estiver se preparando para o ENEM, siga o plano em ENEM Matemática e veja a coleção 10 eBooks.

Perguntas frequentes (FAQ)

Como identificar rapidamente a hipotenusa em um triângulo?

A hipotenusa é o lado oposto ao ângulo de 90°. É sempre o maior lado do triângulo retângulo. Em figuras, costuma estar “em frente” ao quadradinho do ângulo reto.

Quando usar Pitágoras e quando usar trigonometria?

Use Pitágoras para relacionar comprimentos dos lados quando houver ângulo reto. Use trigonometria quando também houver ou precisar de ângulos, como calcular seno, cosseno ou tangente.

Quais são as trincas pitagóricas mais comuns nas provas?

As mais cobradas são (3,4,5), (5,12,13) e (8,15,17). Seus múltiplos também servem, por exemplo (6,8,10) e (10,24,26).

Posso aplicar o Teorema em problemas de coordenadas?

Sim. A distância entre dois pontos é a hipotenusa de um triângulo retângulo cujos catetos são as diferenças nas coordenadas em x e y.

Como organizar os cálculos para ler melhor no celular?

Escreva cada transformação em uma linha, mantendo o “=” alinhado. No site, use blocos com MathJax e quebras de linha como fizemos nos exemplos e soluções.

Autor: Adriano Rocha — Matemática Hoje
Relacionadas

Tipo de Triângulos

Relações Métricas no Triângulo Retângulo

Lei dos Senos

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube