O Teorema de Tales é um dos pilares da Geometria Plana e aparece com frequência no ENEM, em vestibulares e em concursos públicos. Ele relaciona segmentos formados por retas paralelas cortadas por duas transversais, garantindo que esses segmentos sejam proporcionais.
Visualizando o Teorema de Tales
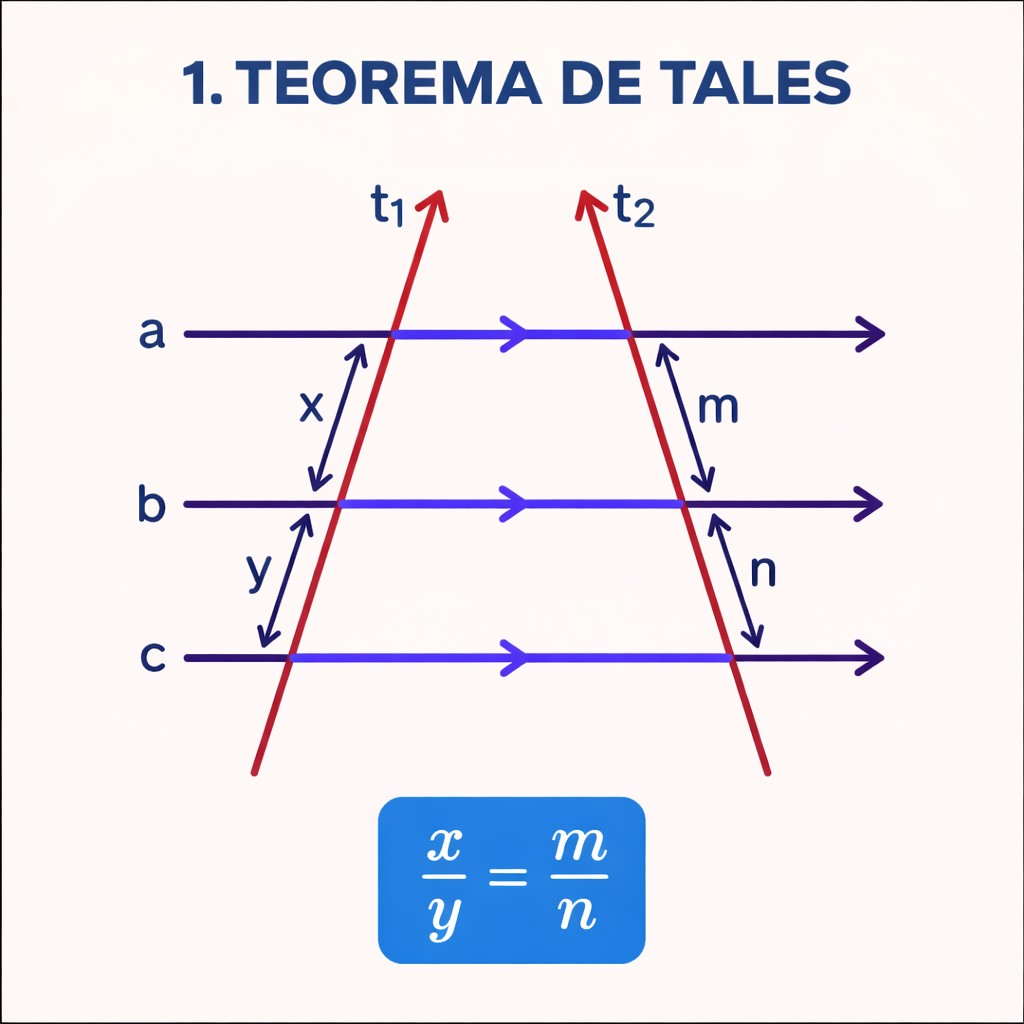
Na figura acima, as retas a, b e c são paralelas, cortadas pelas transversais t₁ e t₂. Elas formam os segmentos:
- x e y na transversal t₁;
- m e n na transversal t₂.
O Teorema de Tales afirma que esses segmentos são proporcionais, isto é:
\(\displaystyle \frac{x}{y} = \frac{m}{n}\)
Entendendo a ideia de proporcionalidade
Dizer que os segmentos são proporcionais significa que a razão entre os comprimentos na primeira transversal é igual à razão entre os comprimentos correspondentes na segunda transversal.
Na prática, se conhecemos três valores, podemos encontrar o quarto usando uma simples regra de três ou produto em cruz.
Exemplo resolvido 1
Problema: Na figura do Teorema de Tales, considere que:
\(\displaystyle \frac{x}{4} = \frac{6}{9}\)
Determine o valor de \(x\).
Resolução passo a passo
- Aplicamos o produto em cruz:
\(x \cdot 9 = 4 \cdot 6\) - Simplificando:
\(9x = 24\) - Isolamos \(x\):
\(x = \dfrac{24}{9}\) - Simplificando a fração:
\(x = \dfrac{8}{3} \approx 2{,}67\)
Resposta: \(x = \dfrac{8}{3}\).
Exemplo resolvido 2
Problema: Duas paralelas cortam duas transversais e formam os segmentos \(x\) e \(5\) em uma transversal, e \(6\) e \(9\) na outra. Sabe-se que:
\(\displaystyle \frac{x}{5} = \frac{6}{9}\)
Encontre o valor de \(x\).
Resolução
- Aplicando o produto em cruz:
\(9x = 5 \cdot 6\) - Multiplicando:
\(9x = 30\) - Dividindo por 9:
\(x = \dfrac{30}{9} = \dfrac{10}{3}\)
Resposta: \(x = \dfrac{10}{3}\).
Exercícios propostos
Resolva os exercícios a seguir para fixar o Teorema de Tales. Eles são ótimos para treinar para o ENEM e para concursos.
- Em duas transversais cortadas por paralelas, temos: \[ \frac{3}{x} = \frac{9}{12}. \] Determine o valor de \(x\).
- Os segmentos em uma transversal medem \(7\) cm e \(x\) cm. Na outra transversal, os segmentos correspondentes medem \(14\) cm e \(18\) cm. Use o Teorema de Tales para encontrar \(x\).
- Num mapa em escala, um trecho de estrada mede 4 cm e corresponde a 20 km na realidade. Outro trecho mede 7 cm no mapa. Qual é o comprimento real desse trecho?
Você pode usar uma regra de três simples em cada item, sempre se lembrando da ideia principal: as razões entre segmentos correspondentes são iguais.
Relação com triângulos semelhantes
O Teorema de Tales está diretamente ligado ao estudo de triângulos semelhantes. Quando traçamos uma reta paralela a um dos lados de um triângulo, formamos um triângulo menor, semelhante ao original. Isso justifica diversos resultados importantes, como o corolário de Tales e o teorema da bissetriz interna.
Se você quiser aprofundar esse tema, vale a pena revisar também os conteúdos de mapas mentais de Geometria, que tornam as relações de semelhança muito mais fáceis de visualizar.
Quer dominar Geometria para ENEM e concursos?
O Teorema de Tales é apenas uma das muitas ferramentas que você precisa para se sentir seguro em questões de Geometria.
- Veja o Curso Matemática Básica: Do Zero à Confiança Prática
- Baixe os 10 eBooks de Matemática para revisão completa
- Acesse as questões resolvidas de Matemática do ENEM
Use esses materiais em conjunto com este artigo e maximize seu aprendizado.
Continue estudando no Matemática Hoje
Se você gostou deste resumo sobre o Teorema de Tales, aproveite para revisar outros conteúdos importantes:
- FGV 2025 – Matemática para Concurso (questões comentadas)
- Mapas Mentais de Matemática para concursos e ENEM
- Entre no grupo gratuito de Matemática no WhatsApp para receber questões e dicas diárias.













