Como aplicar o Teorema do Resto para fatorar polinômios?
Você já se perguntou como descobrir se um número é raiz de um polinômio sem resolver uma equação completa? O Teorema do Resto é uma ferramenta prática para isso. Com ele, é possível determinar raízes, identificar fatores e fatorar polinômios rapidamente — tudo com base em substituições simples e na famosa divisão sintética. Neste artigo, vamos entender o conceito, aplicar o método passo a passo e resolver exemplos reais.
📘 Baixe grátis o eBook Fórmulas de Matemática
Tenha sempre à mão todas as fórmulas de álgebra, funções, trigonometria e geometria para revisar rapidamente.
Baixar eBook gratuitoEntenda o Teorema do Resto com linguagem simples
O teorema afirma que o resto da divisão de \( P(x) \) por \( (x – a) \) é \( P(a) \). Se \( P(a) = 0 \), então \( a \) é uma raiz de \( P(x) \) e \( (x – a) \) é um fator. Isso cria uma “cadeia” de raciocínio: avaliar → detectar raiz → fatorar → reduzir o grau do polinômio.
Se \( P(a) = 0 \Rightarrow a \) é raiz \( \Rightarrow (x – a) \) é fator \( \Rightarrow P(x) = (x – a) \cdot Q(x) \)
Método prático para fatorar polinômios com o teorema
- Teste valores candidatos (divisores do termo independente) e calcule \( P(a) \).
- Achou \( P(a) = 0 \)? Então \( (x – a) \) é fator.
- Faça a divisão sintética de \( P(x) \) por \( (x – a) \) para obter \( Q(x) \).
- Repita o processo com \( Q(x) \) até fatorar completamente.
🧠 Veja também: Mapas Mentais de Matemática
Reveja conteúdos como este de forma visual e prática, com resumos prontos para imprimir.
Acessar Mapas MentaisExemplos resolvidos com o Teorema do Resto
Exemplo 1 — Fatorando um polinômio cúbico
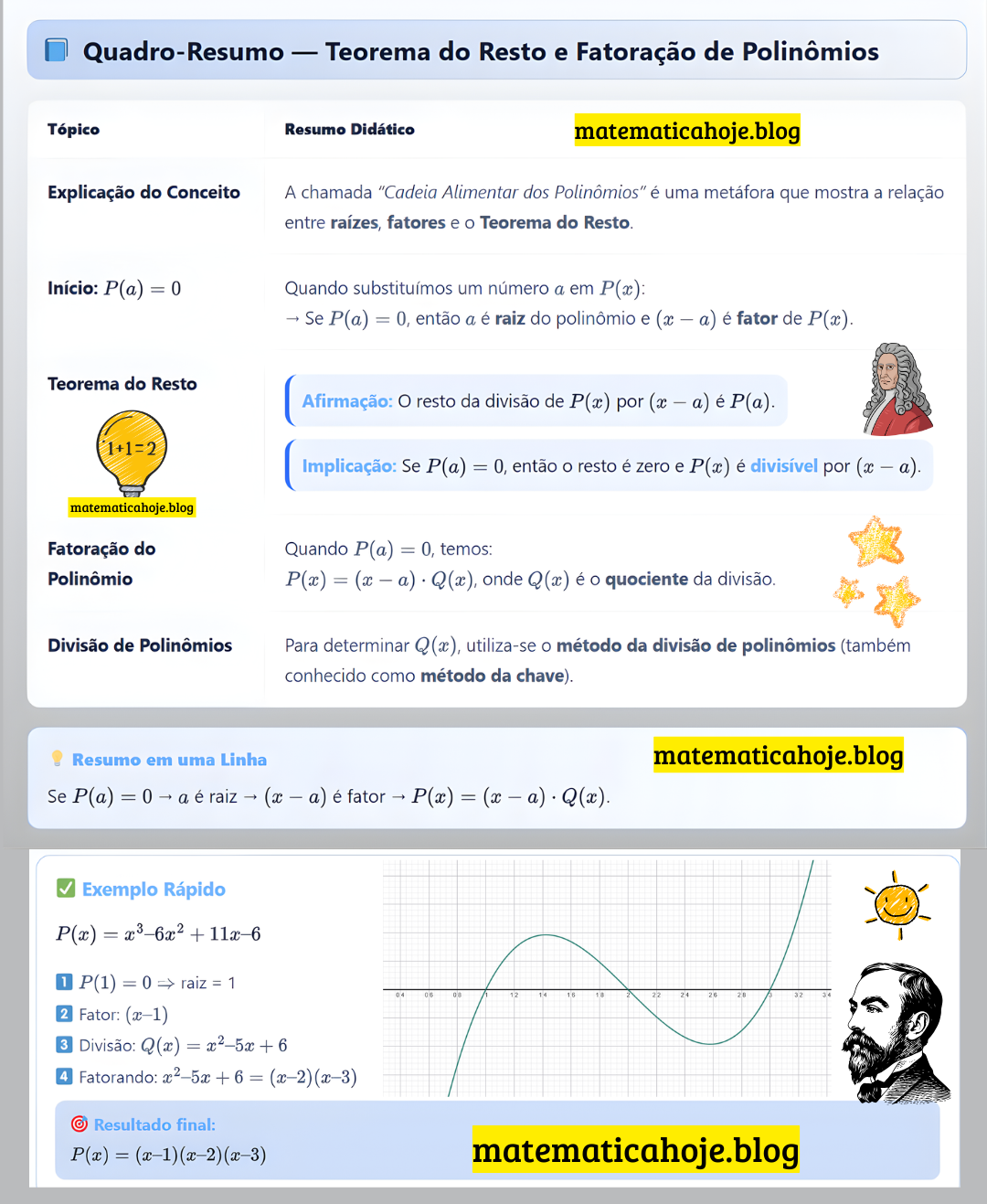
Problema: Fatore \( P(x) = x^3 – 6x^2 + 11x – 6 \)
Teste \( a = 1 \): \( P(1) = 1 – 6 + 11 – 6 = 0 \)
Logo, \( (x – 1) \) é fator.
Dividindo \( P(x) \) por \( (x – 1) \), obtemos \( Q(x) = x^2 – 5x + 6 \)
Fatorando \( Q(x) \): \( Q(x) = (x – 2)(x – 3) \)
Resultado: \( P(x) = (x – 1)(x – 2)(x – 3) \)
Exemplo 2 — Quando o resto não é zero
Problema: Encontre o resto da divisão de \( P(x) = 2x^3 + x^2 – 5x + 3 \) por \( (x – 2) \).
Resto = \( P(2) = 2(8) + 4 – 10 + 3 = 13 \)
Como o resto ≠ 0, \( (x – 2) \) não é fator.
Exemplo 3 — Raiz negativa
Problema: Fatore \( P(x) = x^3 + 2x^2 – 5x – 6 \)
Teste \( a = 2 \): \( P(2) = 8 + 8 – 10 – 6 = 0 \)
Logo, \( (x – 2) \) é fator.
Dividindo, \( Q(x) = x^2 + 4x + 3 \)
Fatorando \( Q(x) = (x + 1)(x + 3) \)
Resultado: \( P(x) = (x – 2)(x + 1)(x + 3) \)
📥 eBook gratuito: Fórmulas de Matemática
Baixe agora o PDF com todas as fórmulas essenciais para o ENEM e concursos.
Baixar eBookAplicações práticas para provas e concursos
- Identificação de raízes reais e complexas de polinômios.
- Simplificação de equações de grau elevado.
- Resolução de questões de fatoração e gráficos de funções.
Continue seus estudos em: ENEM Matemática, 10 eBooks Matemática e Banco de Questões.
Exercícios resolvidos (clique para ver a solução)
1) Fatore \( x^3 – 4x^2 – x + 4 \)
Fator: \( (x – 1) \)
Divisão: \( Q(x) = x^2 – 3x – 4 \)
\( Q(x) = (x – 4)(x + 1) \)
\( P(x) = (x – 1)(x – 4)(x + 1) \)
2) Determine o resto de \( 2x^4 – 3x^3 + 5x – 7 \) por \( (x + 2) \)
3) Mostre que \( (x – 3) \) é fator de \( x^3 – 7x^2 + 14x – 12 \)
Fator: \( (x – 3) \)
Divisão: \( Q(x) = x^2 – 4x + 4 \)
\( Q(x) = (x – 2)^2 \)
\( P(x) = (x – 3)(x – 2)^2 \)
4) Para quais valores de \( a \) o resto da divisão de \( x^2 – ax + 4 \) por \( (x – 2) \) é zero?
\( 8 – 2a = 0 \Rightarrow a = 4 \)
Conclusão
O Teorema do Resto é uma ferramenta poderosa que simplifica a análise e a fatoração de polinômios. Ele conecta substituição, raiz, fatoração e divisão em um único processo. Ao dominar esse método, você ganha agilidade em provas e concursos de Matemática.
Perguntas Frequentes (FAQ)
Como saber se devo usar o Teorema do Resto?
Use quando precisar testar se um número é raiz ou fator de um polinômio sem resolver a equação completa.
O que fazer se o resto for diferente de zero?
Isso significa que o valor testado não é raiz. O número \( P(a) \) obtido é o próprio resto da divisão.
Posso aplicar o método em polinômios de grau maior?
Sim! O Teorema do Resto é válido para qualquer grau. Basta testar sucessivamente as raízes possíveis.
O método da chave é o mesmo que a divisão sintética?
Sim, ambos representam o mesmo processo simplificado de divisão de polinômios do tipo \( P(x) \) por \( (x – a) \).
























