Tipos de Triângulos

Classificação dos triângulos quanto aos lados (equilátero, isósceles e escaleno) e quanto aos ângulos (acutângulo, retângulo e obtusângulo). Inclui propriedades, testes rápidos, exemplos resolvidos e exercícios.

Estude também: Área de Triângulo · Lei dos Senos · Lei do Cosseno · Triângulos — classificação e propriedades.

Classificação quanto aos lados

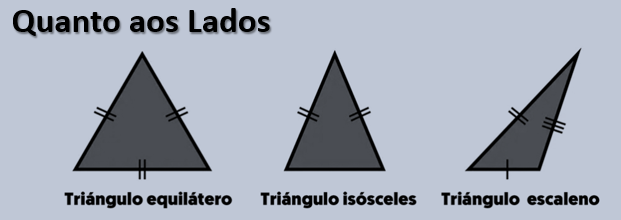
Classificação de triângulos quanto aos lados: equilátero, isósceles e escaleno — Quanto aos lados: equilátero · isósceles · escaleno.

Equilátero 3 lados iguais (e 3 ângulos de \(60^\circ\)).
Área: \(\displaystyle A=\frac{L^2\sqrt{3}}{4}\). Todas as medianas, bissetrizes e alturas coincidem.

Isósceles 2 lados iguais.
Ângulos da base iguais; a altura relativa à base é também mediana e bissetriz. Se base \(a\) e lado igual \(l\), então \(h=\sqrt{l^2-(a/2)^2}\).

Escaleno 3 lados diferentes.
Sem simetrias; valem as propriedades gerais (desigualdade triangular etc.).

\[ \textbf{Desigualdade triangular:}\quad \begin{cases} a

Exemplo 1 — classificação pelos lados

Um triângulo possui lados \(6\), \(6\) e \(5\) cm. Classifique-o quanto aos lados.

Ver solução

Dois lados iguais (\(6=6\)) e o terceiro diferente (\(5\)) ⇒ triângulo isósceles.

Classificação quanto aos ângulos

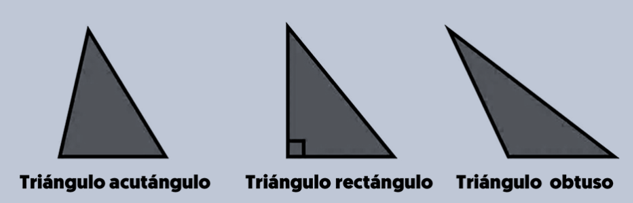
Classificação de triângulos quanto aos ângulos: acutângulo, retângulo e obtusângulo — Quanto aos ângulos: acutângulo · retângulo · obtusângulo.

Acutângulo todos os ângulos são agudos (\(<90^\circ\)).

Retângulo possui um ângulo reto (\(90^\circ\)); lados que o formam são os catetos e o lado oposto é a hipotenusa.

Obtusângulo possui um ângulo obtuso (\(>90^\circ\)).

\[ \textbf{Teste pelo Teorema de Pitágoras (converso):}\ (c=\text{maior lado}) \] \[ a^2+b^2=c^2 \ \Rightarrow\ \text{retângulo} \] \[ a^2+b^2>c^2 \ \Rightarrow\ \text{acutângulo} \] \[ a^2+b^2

Exemplo 2 — classificação pelos ângulos

Um triângulo tem lados \(7\), \(24\) e \(25\) cm. Classifique-o quanto aos ângulos.

Ver solução

\[ \begin{aligned} c&=25 \ (\text{maior lado})\\ 7^2+24^2&=49+576=625\\ c^2&=25^2=625\\ \Rightarrow&\ 7^2+24^2=c^2 \ \Rightarrow\ \textbf{retângulo}. \end{aligned} \]

Propriedades úteis

Soma dos ângulos internos: \(\alpha+\beta+\gamma=180^\circ\).
Medianas intersectam-se no baricentro (divide cada mediana na razão \(2:1\)).
Bissetrizes internas encontram-se no incentro (centro da circunferência inscrita).
Perpendiculares mediatrizes encontram-se no circuncentro (centro da circunferência circunscrita).

Para cálculos, veja: Área de Triângulo, Lei dos Senos, Lei do Cosseno.

Exemplos práticos

Exemplo 3 — área (triângulo retângulo)

Num triângulo retângulo, \(b=12\,\text{cm}\) (base) e \(h=5\,\text{cm}\) (altura). Determine a área.

Ver solução

\[ \begin{aligned} A&=\frac{b\cdot h}{2}\\ &=\frac{12\cdot 5}{2}\\ &=\boxed{30\ \text{cm}^2} \end{aligned} \]

Exemplo 4 — lado e tipo (Lei do Cosseno)

Em um triângulo, \(a=8\), \(b=9\) e o ângulo entre eles é \(\gamma=120^\circ\). Encontre \(c\) e classifique quanto aos ângulos.

Ver solução

\[ \begin{aligned} c^2&=a^2+b^2-2ab\cos\gamma\\ &=8^2+9^2-2\cdot 8\cdot 9\cos120^\circ\\ &=64+81-144\cdot(-\tfrac12)\\ &=145+72=217\\ c&=\sqrt{217}\approx 14{,}73\\ \text{Como }\gamma=120^\circ &>90^\circ,\ \textbf{obtusângulo}. \end{aligned} \]

Lista de exercícios — Tipos de Triângulos

Cada questão tem 5 alternativas. Clique em Mostrar solução para ver o gabarito comentado.

(1)

Os lados de um triângulo medem \(5\), \(5\) e \(8\) cm. Classifique-o quanto aos lados.

Equilátero
Isósceles
Escaleno
Retângulo
Obtusângulo

Mostrar solução

Dois lados iguais ⇒ isósceles. Resposta: B.

(2)

Um triângulo tem lados \(7\), \(9\) e \(12\) cm. Classifique-o quanto aos lados e aos ângulos.

Equilátero e acutângulo
Isósceles e retângulo
Escaleno e obtusângulo
Escaleno e retângulo
Isósceles e obtusângulo

Mostrar solução

\[ c=12,\quad 7^2+9^2=130Resposta: C.

(3)

As medidas \(9\), \(40\) e \(41\) cm formam um triângulo de qual tipo?

Equilátero
Isósceles retângulo
Escaleno retângulo
Escaleno obtusângulo
Isósceles acutângulo

Mostrar solução

\[ 9^2+40^2=81+1600=1681=41^2\Rightarrow \text{retângulo}. \ \text{Lados distintos} \Rightarrow \text{escaleno}. \] Resposta: C.

(4)

Um triângulo equilátero tem lado \(10\) cm. Sua área é:

\(25\sqrt{2}\ \text{cm}^2\)
\(50\ \text{cm}^2\)
\(25\sqrt{3}\ \text{cm}^2\)
\(100\ \text{cm}^2\)
\(10\sqrt{3}\ \text{cm}^2\)

Mostrar solução

\(A=\frac{L^2\sqrt{3}}{4}=\frac{100\sqrt{3}}{4}=25\sqrt{3}\). Resposta: C.

(5)

Num triângulo isósceles, os lados iguais medem \(10\) cm e a base mede \(12\) cm. A área vale:

\(36\ \text{cm}^2\)
\(40\ \text{cm}^2\)
\(45\ \text{cm}^2\)
\(48\ \text{cm}^2\)
\(52\ \text{cm}^2\)

Mostrar solução

\(h=\sqrt{10^2-(12/2)^2}=\sqrt{100-36}=8\). \(A=\frac{12\cdot 8}{2}=48\). Resposta: D.

(6)

Num triângulo retângulo, os catetos valem \(6\) cm e \(8\) cm. A hipotenusa mede:

Mostrar solução

\(c=\sqrt{6^2+8^2}=\sqrt{100}=10\). Resposta: B.

(7)

Os segmentos \(3\), \(4\) e \(8\) cm formam:

Triângulo equilátero
Triângulo isósceles
Triângulo escaleno
Triângulo retângulo
Não formam triângulo

Mostrar solução

\(3+4=7\not>8\). Não satisfaz a desigualdade triangular. Resposta: E.

(8)

Em um triângulo, \(a=7\) cm, \(b=11\) cm e o ângulo entre eles é \(60^\circ\). O lado oposto mede, aproximadamente:

\(8{,}0\ \text{cm}\)
\(9{,}0\ \text{cm}\)
\(9{,}44\ \text{cm}\)
\(9{,}64\ \text{cm}\)
\(10{,}2\ \text{cm}\)

Mostrar solução

\(c^2=7^2+11^2-2\cdot7\cdot11\cos60^\circ=93\Rightarrow c\approx 9{,}64\ \text{cm}\). Resposta: D.

(9)

Um triângulo com lados \(13\), \(14\) e \(15\) cm é:

Isósceles e retângulo
Escaleno e acutângulo
Escaleno e retângulo
Isósceles e obtusângulo
Equilátero

Mostrar solução

\(c=15\). \(13^2+14^2=365>225\Rightarrow\) acutângulo; lados distintos ⇒ escaleno. Resposta: B.

(10)

Num triângulo isósceles, cada ângulo da base mede \(50^\circ\). O ângulo do vértice mede:

\(60^\circ\)
\(70^\circ\)
\(80^\circ\)
\(90^\circ\)
\(100^\circ\)

Mostrar solução

\(50^\circ+50^\circ+\theta=180^\circ \Rightarrow \theta=80^\circ\). Resposta: C.

(11)

No triângulo equilátero de lado \(6\) cm, a altura mede:

\(3\ \text{cm}\)
\(3\sqrt{2}\ \text{cm}\)
\(3\sqrt{3}\ \text{cm}\)
\(6\ \text{cm}\)
\(6\sqrt{3}\ \text{cm}\)

Mostrar solução

\(h=\frac{L\sqrt{3}}{2}=\frac{6\sqrt{3}}{2}=3\sqrt{3}\). Resposta: C.

(12)

Num triângulo retângulo, a hipotenusa é \(13\) cm e um cateto mede \(5\) cm. O outro cateto mede:

\(10\ \text{cm}\)
\(11\ \text{cm}\)
\(12\ \text{cm}\)
\(13\ \text{cm}\)
\(14\ \text{cm}\)

Mostrar solução

\(b=\sqrt{13^2-5^2}=\sqrt{169-25}=\sqrt{144}=12\ \text{cm}\). Resposta: C.

Resumo rápido

\[ \textbf{Área (geral):}\quad A=\frac{b\cdot h}{2} \]

\[ \textbf{Heron:}\quad A=\sqrt{s(s-a)(s-b)(s-c)},\ \ s=\frac{a+b+c}{2} \]

\[ \textbf{Lei dos Senos:}\quad \frac{a}{\sin\alpha}=\frac{b}{\sin\beta}=\frac{c}{\sin\gamma}=2R \]

\[ \textbf{Lei do Cosseno:}\quad c^2=a^2+b^2-2ab\cos\gamma \quad(\text{análogas para } a,b) \]

Continue com: Área de Triângulo · Lei dos Senos · Lei do Cosseno.

Tipo de Triângulos

Tipos de Triângulos

Classificação quanto aos lados

Exemplo 1 — classificação pelos lados

Classificação quanto aos ângulos

Exemplo 2 — classificação pelos ângulos

Propriedades úteis

Exemplos práticos

Exemplo 3 — área (triângulo retângulo)

Exemplo 4 — lado e tipo (Lei do Cosseno)

Lista de exercícios — Tipos de Triângulos

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

Resumo rápido

Materiais do Matemática Hoje

Triângulo Escaleno

Área de Triângulo

Triângulo Retângulo

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Sequências

Exercício Progressão Geométrica

Progressão Geométrica (PG)

Exercício Estatística

Pontos Notáveis do Triângulo

Exercício Pontos Notáveis do Triângulo

📘 Baixe Grátis o eBook de Fórmulas Matemática

📘 Mapas Mentais

📚 10 E-books de Matemática

Questões

Conteúdo

Banca