Triângulo Circunferência (Incírculo no Triângulo)

Incírculo: círculo tangente aos três lados. Centro = incentro (interseção das bissetrizes internas). Raio = \(r\).

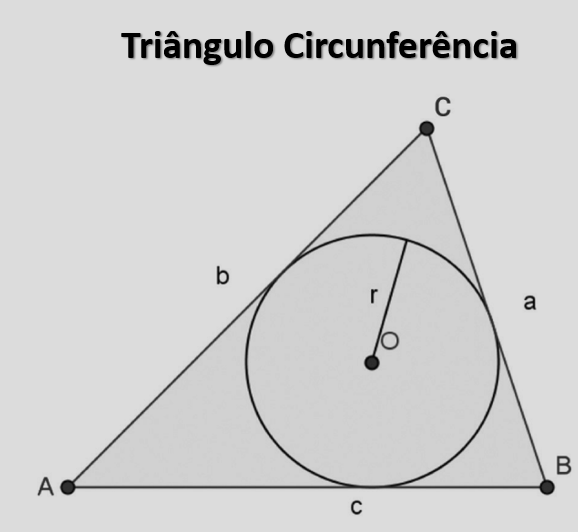
SEO discreto: triângulo circunferência, incírculo, incentro, raio \(r\), semiperímetro \(s\), área \(A=rs\).

Definição e objetos notáveis

Incírculo: círculo inscrito no triângulo, tangente aos três lados.
Incentro: encontro das bissetrizes internas; é o centro do incírculo.
Raio do incírculo: \(r\), distância do incentro a cada lado.
Pontos de tangência: se o lado oposto a \(A\) mede \(a\), os segmentos criados pelo ponto de tangência são \(s-b\) e \(s-c\).

As fórmulas valem para qualquer triângulo: equilátero, isósceles ou escaleno.

Propriedades e fórmulas essenciais

Semiperímetro: \( \displaystyle s=\frac{a+b+c}{2} \). Área por incírculo: \( \displaystyle A=rs \quad \Rightarrow \quad r=\frac{A}{s} \). Heron: \( \displaystyle A=\sqrt{s(s-a)(s-b)(s-c)} \). Meia-ângulos: \( \displaystyle \tan\frac{A}{2}=\frac{r}{s-a},\ \tan\frac{B}{2}=\frac{r}{s-b},\ \tan\frac{C}{2}=\frac{r}{s-c}. \) Ligação com a circunferência circunscrita (raio \(R\)): \( \displaystyle r=4R\sin\frac{A}{2}\sin\frac{B}{2}\sin\frac{C}{2} \).

Centros e posições: veja Pontos Notáveis do Triângulo. Compare com classificações por ângulos: retângulo, acutângulo, obtusângulo. Panorama geral: tipos de triângulos.

Exemplos resolvidos (passo a passo vertical)

Exemplo 1 — O incírculo tem raio \(r=3\) e semiperímetro \(s=14\). Calcule a área.

Mostrar solução

\(A=rs\)
\(=3\cdot 14\)
\(=42\).

Exemplo 2 — Para lados \(a=7\), \(b=8\), \(c=9\), determine \(r\).

Mostrar solução

\(s=\dfrac{7+8+9}{2}\)
\(=12\)

\(A=\sqrt{12(12-7)(12-8)(12-9)}\)
\(=\sqrt{12\cdot 5\cdot 4\cdot 3}\)
\(=12\sqrt5\)

\(r=\dfrac{A}{s}\)
\(=\dfrac{12\sqrt5}{12}\)
\(=\sqrt5\approx 2{,}236\).

Exemplo 3 — Num triângulo com lados \(a=13\), \(b=14\), \(c=15\), ache os segmentos no lado \(a\) criados pelo ponto de tangência.

Mostrar solução

\(s=\dfrac{13+14+15}{2}\)
\(=21\)

No lado \(a=13\), os segmentos são \(s-b=21-14=7\) e \(s-c=21-15=6\).

Verificação: \(7+6=13\).

Exemplo 4 — Para o triângulo do Ex.3, calcule \(\tan\frac{A}{2}\).

Mostrar solução

\(\tan\frac{A}{2}=\dfrac{r}{s-a}\). Como \(A\) pertence ao lado \(a=13\) e \(s=21\), primeiro obtemos \(r=\dfrac{A}{s}=\dfrac{84}{21}=4\) (pois \(A=\sqrt{21\cdot8\cdot7\cdot6}=84\)).
\(\tan\frac{A}{2}=\dfrac{4}{21-13}=\dfrac{4}{8}=\dfrac{1}{2}=0{,}5\).

Exemplo 5 — Em um triângulo retângulo com catetos 6 e 8, determine \(r\).

Mostrar solução

Hipotenusa \(=10\), \(A=\dfrac{6\cdot8}{2}=24\), \(s=\dfrac{6+8+10}{2}=12\).
\(r=\dfrac{A}{s}=\dfrac{24}{12}=2\).

Exercícios de múltipla escolha (com solução em abre/fecha)

1) Se \(r=2\) e \(s=21\), então a área é:

A) 20 B) 42 C) 24 D) 48 E) 10

Mostrar solução

\(A=rs\)
\(=2\cdot 21\)
\(=42\).

2) Para \(a=7\), \(b=8\), \(c=9\), o valor de \(r\) é, aprox.:

A) 1,9 B) 2,24 C) 2,50 D) 2,80

Mostrar solução

\(r=\sqrt5\approx 2{,}236\Rightarrow\) opção B.

3) Em geral, o raio do incírculo satisfaz:

A) \(r=\dfrac{s}{A}\) B) \(r=\dfrac{a+b+c}{A}\) C) \(r=\dfrac{A}{s}\) D) \(r=A\cdot s\)

Mostrar solução

Da fórmula da área \(A=rs\Rightarrow r=A/s\). Alternativa C.

4) Para lados \(13,14,15\), os segmentos no lado de medida \(13\) são:

A) 6 e 8 B) 5 e 7 C) 7 e 6 D) 4 e 9

Mostrar solução

\(s=21\Rightarrow s-b=7,\ s-c=6\). Alternativa C.

5) Se \(s=18\) e \(r=3\), o perímetro vale:

A) 30 B) 36 C) 27 D) 42

Mostrar solução

Perímetro \(P=2s=36\). Alternativa B.

6) Em um triângulo retângulo de catetos 6 e 8, o raio do incírculo é:

A) 1 B) 2 C) 3 D) 4

Mostrar solução

Do Exemplo 5: \(r=\dfrac{24}{12}=2\). Alternativa B.

7) Se \(A=60^\circ\), \(B=70^\circ\), \(C=50^\circ\) e \(R=10\), então \(r\approx\):

A) 3,9 B) 4,5 C) 4,85 D) 5,2

Mostrar solução

\(r=4R\sin30^\circ\sin35^\circ\sin25^\circ\)
\(\approx 40\cdot 0{,}5\cdot 0{,}5736\cdot 0{,}4226\)
\(\approx 4{,}85\). Alternativa C.

8) A relação correta envolvendo meia-ângulos é:

A) \( \tan\frac{A}{2}=\dfrac{s}{r} \) B) \( \tan\frac{A}{2}=\dfrac{r}{s-a} \) C) \( \sin\frac{A}{2}=\dfrac{r}{s} \) D) \( \cos\frac{A}{2}=\dfrac{r}{a} \)

Mostrar solução

Por definição geométrica do incentro: \(\tan\frac{A}{2}=\dfrac{r}{s-a}\). Alternativa B.

9) Dado \(r=2{,}5\) e \(s=19\), o perímetro do triângulo é:

A) 34 B) 38 C) 40 D) 42

Mostrar solução

Perímetro \(P=2s=38\). Alternativa B.

10) O incentro é a interseção de:

A) Mediatrizes B) Medianas C) Alturas D) Bissetrizes internas

Mostrar solução

Definição: incentro = encontro das bissetrizes internas. Alternativa D.