O Triângulo de Pascal é uma das estruturas numéricas mais importantes da Matemática. Ele aparece na álgebra, na combinatória, na probabilidade e em diversos contextos onde relações entre números revelam padrões fundamentais.
Neste artigo, vamos entender como o triângulo é construído, qual é a lógica por trás de seus valores e por que ele produz exatamente os coeficientes usados no Binômio de Newton.
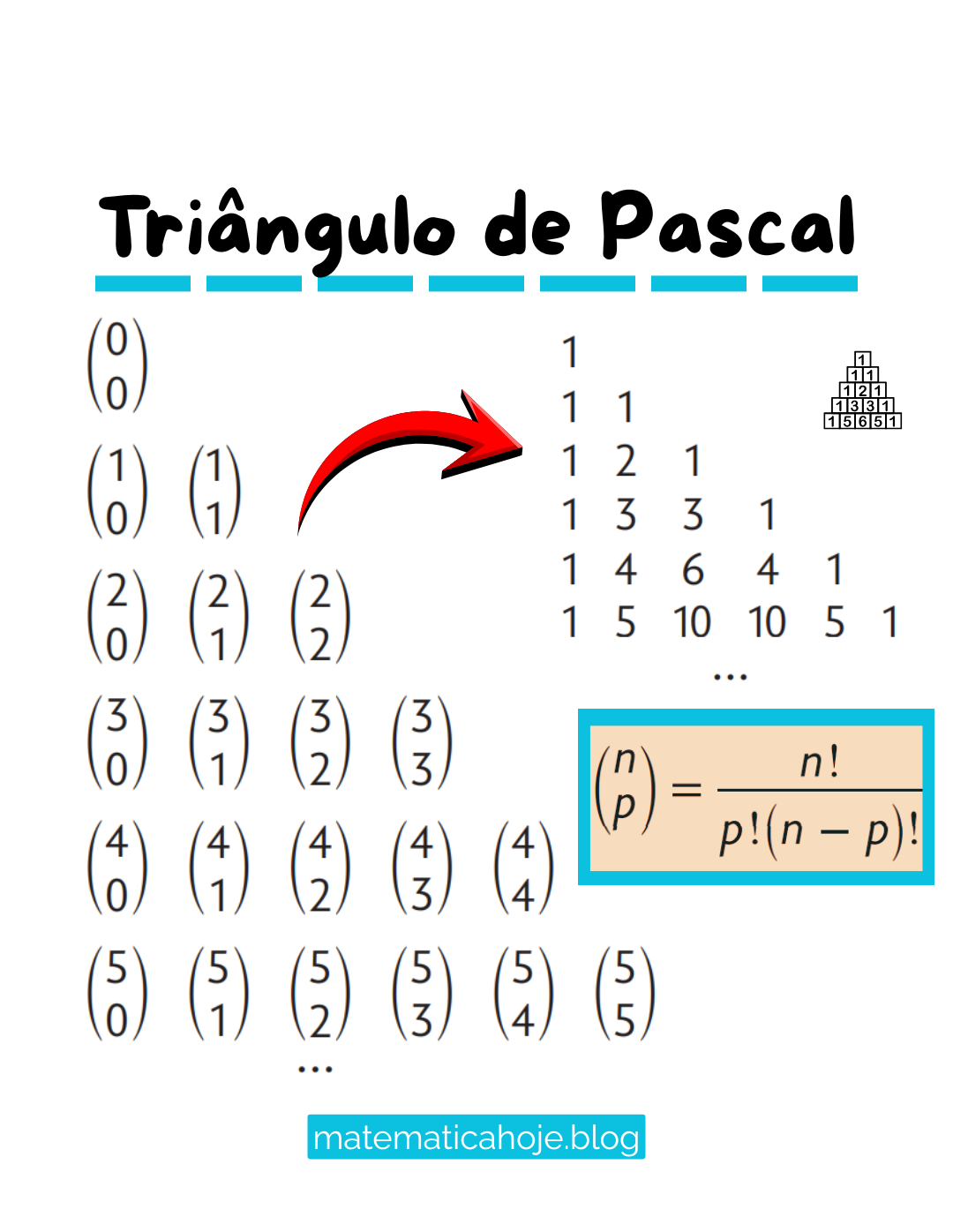
Como o Triângulo de Pascal é construído?
O triângulo começa com o número 1 no topo. A partir daí, cada linha representa os coeficientes associados às potências de um binômio.
As regras de construção são:
- o primeiro e o último número de cada linha são sempre 1;
- cada número interno é a soma dos dois números diretamente acima.
Assim, a linha correspondente ao valor \(n\) contém exatamente os coeficientes binomiais \(\binom{n}{p}\) para \(p = 0,1,2,\dots,n\).
Por que os números do Triângulo de Pascal são coeficientes binomiais?
Cada elemento do triângulo cumpre a seguinte relação recursiva:
Essa é exatamente a definição recursiva dos coeficientes binomiais. Por isso, o Triângulo de Pascal reproduz naturalmente os mesmos valores usados em contagem, combinatória e na expansão de binômios.
Relação com o Binômio de Newton
A linha correspondente ao valor n no Triângulo de Pascal contém exatamente os coeficientes necessários para o desenvolvimento de:
Por exemplo, a expansão de \((x + y)^5\) utiliza exatamente a linha 5 do triângulo, cujos coeficientes são: \(1, 5, 10, 10, 5, 1\).
Para aprofundar esse estudo, veja também: Fórmula em Somatório do Binômio de Newton .
Fórmula geral para os coeficientes
Cada entrada \(\binom{n}{p}\) pode ser calculada através da fórmula:
Isso permite calcular qualquer número do Triângulo de Pascal, mesmo sem construir o triângulo completo.
Exemplo prático: construindo a linha 6
Objetivo: montar a linha 6 do triângulo.
Usando a fórmula dos coeficientes binomiais:
\(\binom{6}{0} = 1\) \(\binom{6}{1} = 6\) \(\binom{6}{2} = 15\) \(\binom{6}{3} = 20\) \(\binom{6}{4} = 15\) \(\binom{6}{5} = 6\) \(\binom{6}{6} = 1\)
Linha 6: 1, 6, 15, 20, 15, 6, 1
Esta linha é utilizada no desenvolvimento de (x + y)6, conforme estudado no Termo Geral do Binômio de Newton .
Aplicações do Triângulo de Pascal
O triângulo aparece em muitas áreas da Matemática:
- desenvolvimento de binômios;
- probabilidade (distribuições binomiais);
- combinatória;
- contagem de caminhos em malhas;
- estudo de padrões e simetrias numéricas.
Por isso, compreender o Triângulo de Pascal facilita o aprendizado de diversos conteúdos avançados.
O Triângulo de Pascal é muito mais do que um arranjo de números: ele funciona como uma verdadeira “máquina combinatória”, revelando padrões, simetrias e relações fundamentais presentes na Matemática.