Triângulos — tipos e propriedades
Este guia reúne a classificação dos triângulos (por lados e por ângulos), as propriedades fundamentais, os pontos notáveis, critérios de congruência e semelhança, além de fórmulas úteis de perímetro, área e relações trigonométricas. No final, você encontra exemplos resolvidos e exercícios.
Classificação dos triângulos
Por ângulos
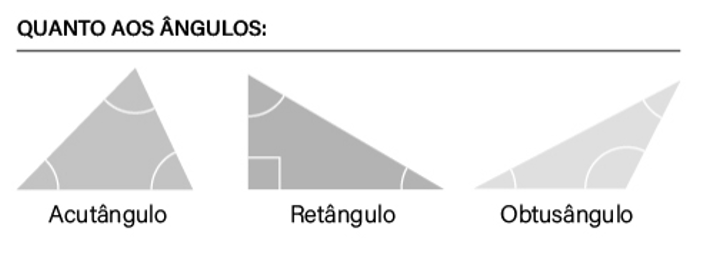
Por lados
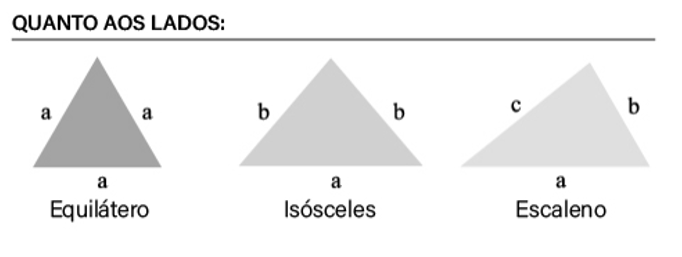
Propriedades fundamentais
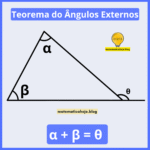
Ângulo externo: em qualquer vértice, é igual à soma dos dois internos não adjacentes.
Dica de prova e ENEM: a desigualdade triangular é essencial para checar se três segmentos podem formar triângulo e para classificar ângulos (via lei dos cossenos).
Congruência e semelhança
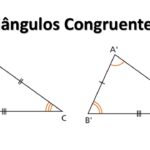
Congruência (triângulos “iguais”): critérios — LAL (SAS), ALA (ASA), LLL (SSS) e, para retângulos, hipotenusa–cateto.
Semelhança (mesma forma, escala diferente): critérios — AA (dois ângulos), LAL proporcional e LLL proporcional.
Pontos notáveis e elementos
- Mediatriz (perpendicular no meio do lado) → concorrência no circuncentro; centro da circunferência circunscrita (raio \(R\)).
- Bissetriz (divide o ângulo em dois) → concorrência no incentro; centro da circunferência inscrita (raio \(r\)).
- Mediana (une vértice ao ponto médio do lado oposto) → concorrência no baricentro; divide cada mediana na razão \(2:1\).
- Altura (perpendicular ao lado oposto) → concorrência no ortocentro.
Aqui, \(A\) é a área e \(s\) é o semiperímetro. Para mais detalhes, veja Área do Triângulo.
Relações trigonométricas
Estude os tópicos dedicados: Lei dos Senos e Lei dos Cossenos.
Perímetro, área e fórmulas úteis
Para casos específicos (retângulo, obtusângulo, equilátero, usando \(R\) ou \(r\)), veja: Área do Triângulo — guia completo.
Exemplos resolvidos (situação-problema)
Classificação por lados e ângulos
- Cenário
- Uma peça triangular tem lados \(a=7\text{ cm}\), \(b=9\text{ cm}\), \(c=12\text{ cm}\).
- Dados
- Três medidas de lados.
Pergunta: a peça é equilátera, isósceles ou escalena? É acutângula, retângula ou obtusângula?
Ver solução
Ponto notável e relação com a área
- Cenário
- No triângulo \(ABC\), \(a=10\), \(b=13\), \(c=15\).
- Dados
- Calcular \(A\), \(s\) e o raio \(r\) da circunferência inscrita.
Pergunta: encontre \(A\), \(s\) e \(r\) usando Heron e \(A=r\cdot s\).
Ver solução
Semelhança para encontrar medida desconhecida
- Cenário
- Dois triângulos têm \(\widehat{A}=\widehat{A’}\) e \(\widehat{B}=\widehat{B’}\). Em \(ABC\), \(AB=8\), \(AC=10\). Em \(A’B’C’\), \(A’B’=12\).
- Dados
- Semelhança por AA, razão de semelhança \(k\).
Pergunta: determine \(A’C’\).
Ver solução
Exercícios propostos (situação-problema)
Classificação por ângulo via cossenos
- Cenário
- Peça com lados \(a=5\), \(b=6\), \(c=8\).
- Dados
- Lados do triângulo.
Pergunta: classifique quanto ao ângulo (acutângulo/retângulo/obtusângulo).
Ver gabarito
Verificar existência (desigualdade triangular)
- Cenário
- Segmentos \(7\), \(10\), \(18\).
- Dados
- Três medidas.
Pergunta: formam triângulo? Se sim, qual a classificação por lados?
Ver gabarito
Área por Heron e classificação por lados
- Cenário
- Estrutura metálica com lados \(8\), \(9\), \(9\).
- Dados
- Dois lados iguais.
Pergunta: calcule a área e classifique por lados.
Ver gabarito
Semelhança e razão de escala
- Cenário
- Modelos reduzidos de um telhado triangular.
- Dados
- Triângulos semelhantes com razão \(k=0{,}8\). O original tem lado \(a=12\).
Pergunta: quanto mede o lado correspondente no modelo?
Ver gabarito
Continue estudando
• Tudo sobre Triângulos: classificação e propriedades (artigo complementar com visão ampliada).
• Área do Triângulo — base–altura, 2 lados + ângulo, Heron, circunrádio/inrádio.
• Lei dos Senos e Lei dos Cossenos — relações para triângulos quaisquer.
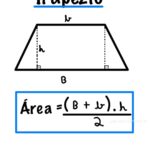
• Área do Trapézio — reforço de geometria plana com situações-problema.