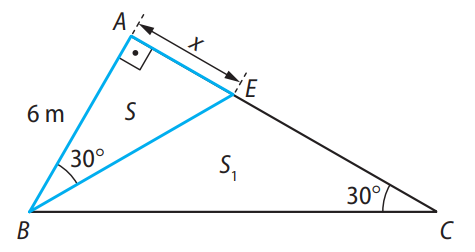
(UEA-AM) Um jardim, representado na figura pelo triângulo retângulo \( ABC \), foi dividido em dois canteiros, \( S \) e \( S_1 \), por uma grade, indicada pelo segmento \( BE \).
Sabendo que \( AB = 6 \, m \), o perímetro do triângulo \( ABE \) é igual a:
a) \( 4 + 10 \sqrt{3} \, m \).
b) \( 12 \sqrt{3} \, m \).
c) \( 6 + 6 \sqrt{3} \, m \).
d) \( 14 \sqrt{3} \, m \).
e) \( 6 + 10 \sqrt{3} \, m \).
No triângulo \( ABE \), aplicando a tangente do ângulo de \( 30^\circ \), temos:
Agora, aplicando o Teorema de Pitágoras para determinar \( BE \):
O perímetro de \( \triangle ABE \) será:
Resposta correta: alternativa c.
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












