Em praticamente todas as provas de Matemática do ensino fundamental, do ensino médio e também em concursos, aparece algum problema envolvendo um triângulo retângulo e as famosas relações trigonométricas: seno, cosseno e tangente. Se você entende bem essa figura e sabe “quem é cateto oposto, cateto adjacente e hipotenusa”, muitos exercícios se tornam questões de substituição de valores em fórmulas simples.
1. Entendendo o triângulo retângulo da imagem
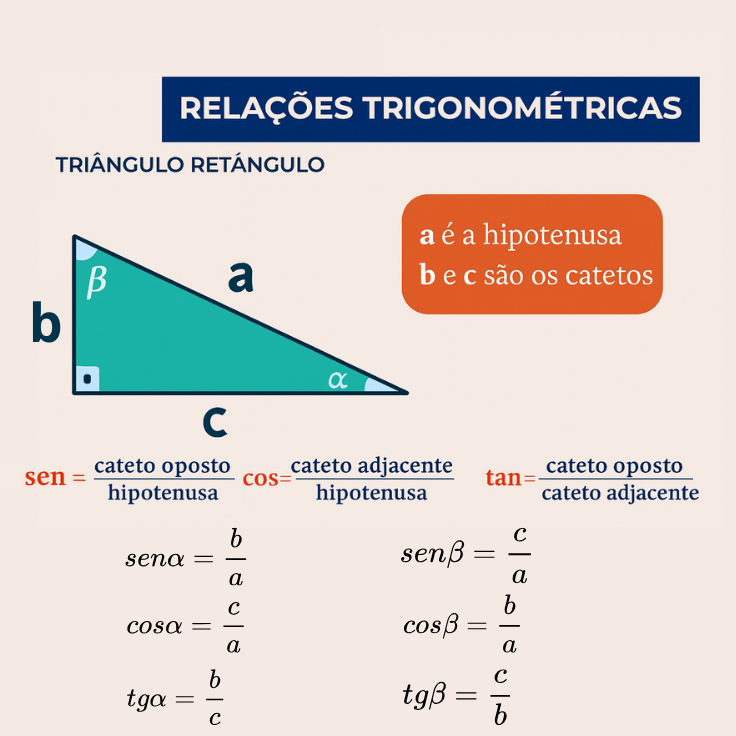
Observe o triângulo retângulo destacado na imagem. Ele tem um ângulo de 90° (o quadradinho indica o ângulo reto) e dois outros ângulos agudos, que foram chamados de α (alfa) e β (beta).
Os lados receberam as letras a, b e c:
- a é a hipotenusa – o lado que fica em frente ao ângulo reto;
- b e c são os catetos – os dois lados que formam o ângulo de 90°.
Em qualquer triângulo retângulo, a hipotenusa é sempre o maior lado e, na trigonometria básica, toda a construção das relações de seno e cosseno é feita a partir dela.
Hipotenusa: lado oposto ao ângulo reto. Catetos: lados que formam o ângulo reto.
Um erro comum que vejo em sala de aula é o aluno decorar fórmulas, mas não olhar para o desenho: ele não identifica qual lado é quem. Por isso, sempre que surgir uma questão, o primeiro passo é repetir mentalmente: “a é a hipotenusa; b e c são os catetos” e marcar isso na figura.
2. Cateto oposto, cateto adjacente e hipotenusa
Depois que você identificou quem é a hipotenusa, falta decidir qual cateto é oposto e qual é adjacente ao ângulo que está sendo analisado.
Para um ângulo qualquer do triângulo retângulo, valem estas ideias:
- cateto oposto: é o lado que fica “na frente” do ângulo, sem tocar nele;
- cateto adjacente: é o cateto que está “encostado” no ângulo;
- a hipotenusa é sempre a mesma, independentemente do ângulo escolhido.
Na figura, se olharmos para o ângulo α (na base):
- o cateto oposto a α é o lado b;
- o cateto adjacente a α é o lado c;
- a hipotenusa continua sendo a.
Já para o ângulo β (no topo do triângulo):
- o cateto oposto a β é o lado c;
- o cateto adjacente a β é o lado b;
- a hipotenusa permanece a.
Perceba que o mesmo lado pode ser oposto a um ângulo e adjacente a outro, dependendo de quem estamos observando. É exatamente essa mudança que gera muitas dúvidas em exercícios com sen, cos e tg.
3. Definições de seno, cosseno e tangente no triângulo retângulo
Agora que você já sabe identificar os lados em relação a cada ângulo, podemos escrever as definições das relações trigonométricas básicas:
Seno de um ângulo agudo (no triângulo retângulo): \(\mathrm{sen}(\theta) = \dfrac{\text{cateto oposto}}{\text{hipotenusa}}\)
Cosseno de um ângulo agudo: \(\mathrm{cos}(\theta) = \dfrac{\text{cateto adjacente}}{\text{hipotenusa}}\)
Tangente de um ângulo agudo: \(\mathrm{tg}(\theta) = \dfrac{\text{cateto oposto}}{\text{cateto adjacente}}\)
Essas três frações são a base da trigonometria no ensino básico. Quase todas as questões de triângulo retângulo vão pedir que você use uma delas para descobrir uma medida desconhecida.
4. Fórmulas para o ângulo α
Vamos aplicar as definições diretamente no triângulo da imagem, começando pelo ângulo α.
Relembrando:
- cateto oposto a α → b;
- cateto adjacente a α → c;
- hipotenusa → a.
Substituindo nas fórmulas gerais, obtemos:
\(\mathrm{sen}\,\alpha = \dfrac{b}{a}\)
\(\mathrm{cos}\,\alpha = \dfrac{c}{a}\)
\(\mathrm{tg}\,\alpha = \dfrac{b}{c}\)
Imagine, por exemplo, que em um problema de Física você tenha um plano inclinado formando o ângulo α com o chão, a hipotenusa representando o trilho tem comprimento \(a = 10\) metros, e o cateto oposto (altura) vale \(b = 6\) metros. Para descobrir o seno desse ângulo, basta aplicar:
\(\mathrm{sen}\,\alpha = \dfrac{b}{a} = \dfrac{6}{10} = 0{,}6\)
Esse tipo de raciocínio aparece quando calculamos componentes de forças, altura de rampas acessíveis ou mesmo quando um exercício de vestibular pede o “coeficiente de atrito” em função do ângulo da rampa.
5. Fórmulas para o ângulo β
Agora vamos repetir o mesmo raciocínio para o ângulo β.
- cateto oposto a β → c;
- cateto adjacente a β → b;
- hipotenusa → a.
Substituindo nas fórmulas, temos:
\(\mathrm{sen}\,\beta = \dfrac{c}{a}\)
\(\mathrm{cos}\,\beta = \dfrac{b}{a}\)
\(\mathrm{tg}\,\beta = \dfrac{c}{b}\)
Note que algumas frações “se inverteram” em relação ao ângulo α. Isso acontece porque trocamos quem é cateto oposto e quem é cateto adjacente. Um mesmo triângulo permite enxergar duas famílias de relações trigonométricas, dependendo de qual dos ângulos agudos está sendo considerado.
Em situações do cotidiano, esse tipo de troca aparece em problemas de observação de objetos em diferentes posições. Por exemplo, ao calcular o ângulo com que uma câmera de segurança deve ser inclinada para filmar um ponto do chão, às vezes o triângulo é montado em torno do ângulo no chão (α), outras vezes em torno do ângulo junto à câmera (β). O triângulo é o mesmo, mas as fórmulas mudam de lugar.
6. Exemplo completo com cálculo de lados e razões trigonométricas
Vamos considerar agora um triângulo retângulo em que a hipotenusa mede \(a = 13\) cm, o cateto vertical é \(b = 5\) cm e o cateto da base é \(c = 12\) cm. Esse conjunto de números é muito utilizado em problemas, porque satisfaz o teorema de Pitágoras: \(5^2 + 12^2 = 25 + 144 = 169 = 13^2\).
Para o ângulo α (na base), as razões ficam:
\(\mathrm{sen}\,\alpha = \dfrac{b}{a} = \dfrac{5}{13}\)
\(\mathrm{cos}\,\alpha = \dfrac{c}{a} = \dfrac{12}{13}\)
\(\mathrm{tg}\,\alpha = \dfrac{b}{c} = \dfrac{5}{12}\)
Já para o ângulo β (no topo), trocamos o papel dos catetos:
\(\mathrm{sen}\,\beta = \dfrac{c}{a} = \dfrac{12}{13}\)
\(\mathrm{cos}\,\beta = \dfrac{b}{a} = \dfrac{5}{13}\)
\(\mathrm{tg}\,\beta = \dfrac{c}{b} = \dfrac{12}{5}\)
Em uma questão típica de prova, o enunciado pode apresentar apenas os valores numéricos e pedir, por exemplo, “calcule o seno de α” ou “determine a tangente de β”. Ao enxergar o triângulo e as relações, você rapidamente identifica qual fração precisa ser montada e evita contas desnecessárias.
Mapas mentais para organizar as relações trigonométricas
Se você gosta de visualizar tudo de forma resumida, com esquemas e setas ligando os conceitos, vale a pena conhecer os mapas mentais de Matemática do projeto Matemática Hoje. Eles ajudam a fixar rapidamente quem é cateto oposto, adjacente, hipotenusa e como aparecem as fórmulas de seno, cosseno e tangente.
Clique para conferir: Mapas mentais de Matemática – Matemática Hoje .
7. Aplicando as relações trigonométricas em situações do dia a dia
As relações trigonométricas não servem apenas para “fazer conta” em prova. Elas aparecem em várias situações práticas:
- cálculo de altura de prédios usando a sombra e o ângulo de elevação do Sol;
- dimensionamento de rampas de acessibilidade e escadas;
- estudo de forças em planos inclinados na Física;
- problemas de navegação e localização com ângulos de visada.
Imagine que você está em frente a um prédio e sabe que o ponto onde está é distante 20 metros da base dele. Com um aplicativo de medição de ângulo, você descobre que a linha de visão até o topo forma um ângulo de \(30^\circ\) com o chão. Se representarmos essa situação por um triângulo retângulo, o lado “20 m” será o cateto adjacente ao ângulo e a altura do prédio será o cateto oposto.
Usando seno ou tangente, conseguimos aproximar essa altura:
\(\mathrm{tg}(30^\circ) = \dfrac{\text{altura}}{20}\)
\(\text{altura} = 20 \cdot \mathrm{tg}(30^\circ)\)
Em muitos concursos, a questão já traz o valor aproximado de \(\mathrm{tg}(30^\circ)\) e você só precisa fazer a multiplicação. A lógica é sempre a mesma: identificar quem é cateto oposto, adjacente e hipotenusa, escolher a relação correta (sen, cos ou tg) e substituir os valores.
Fórmulas de trigonometria sempre à mão (material gratuito)
Para não esquecer nenhuma relação, é muito útil ter um resumo pronto para consulta rápida. O eBook de Fórmulas de Matemática do Matemática Hoje traz as principais fórmulas de trigonometria, geometria, álgebra e muito mais, em formato enxuto e objetivo.
Você pode fazer o download gratuito em: eBook Fórmulas de Matemática – Download grátis .
8. Conclusão: como dominar de vez as relações trigonométricas
Para dominar as relações trigonométricas no triângulo retângulo, o segredo não é decorar fórmulas soltas, mas entender o desenho. Sempre comece identificando a hipotenusa, depois veja quem é cateto oposto e quem é cateto adjacente em relação ao ângulo estudado. A partir daí, as expressões \(\mathrm{sen}\,\theta = \dfrac{\text{oposto}}{\text{hipotenusa}}\), \(\mathrm{cos}\,\theta = \dfrac{\text{adjacente}}{\text{hipotenusa}}\) e \(\mathrm{tg}\,\theta = \dfrac{\text{oposto}}{\text{adjacente}}\) passam a fazer muito mais sentido.
Com prática em exercícios de livros, provas anteriores e situações do cotidiano, você vai perceber que problemas que antes pareciam difíceis se tornam apenas uma questão de montar a fração correta e fazer uma conta de divisão.
Sempre que se deparar com um novo exercício, lembre-se do triângulo da imagem: a é a hipotenusa, b e c são os catetos, e as relações de seno, cosseno e tangente organizam tudo o que você precisa saber sobre os ângulos α e β.