TRONCO DE CONE – Geometria Espacial

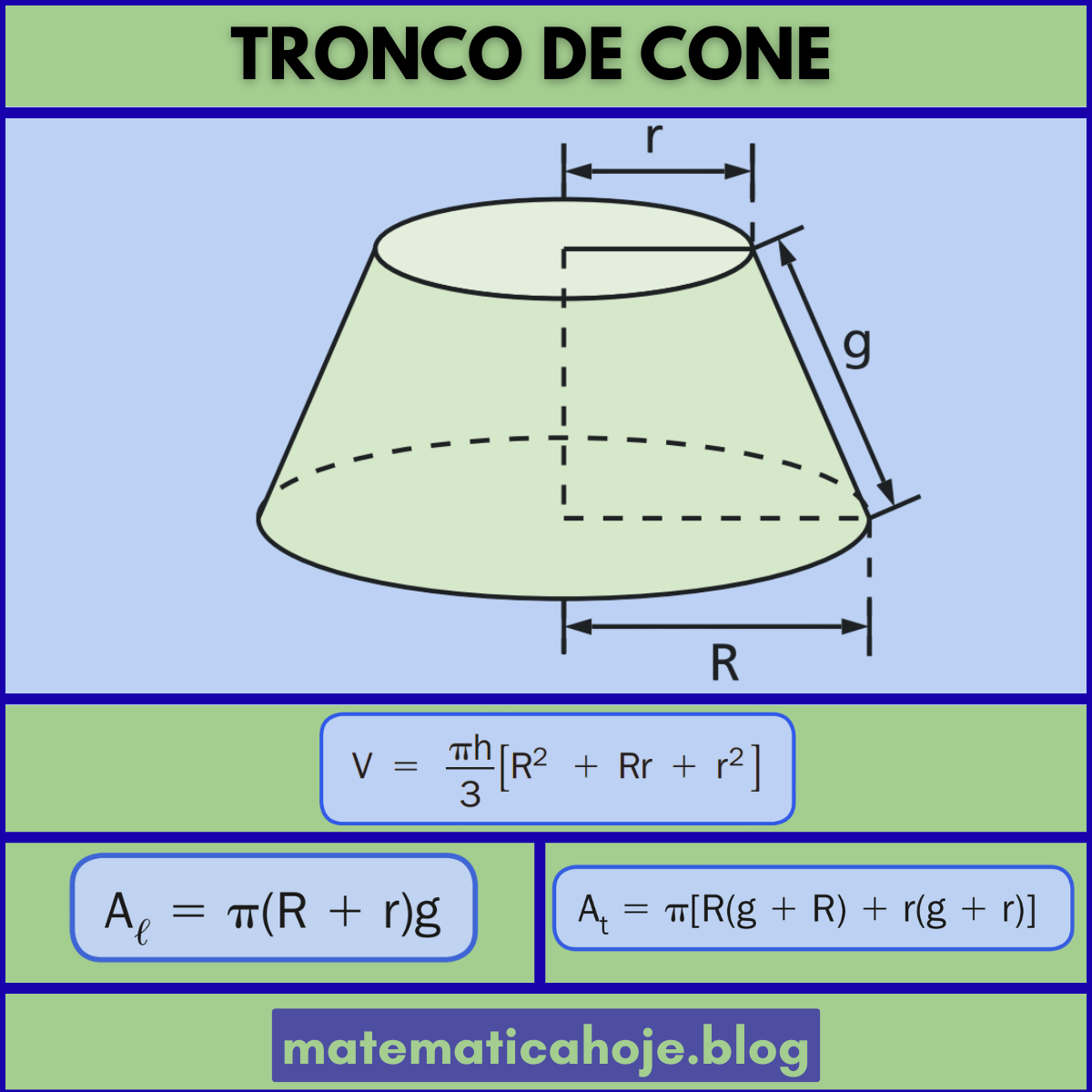
Tronco de cone com raios R (base maior), r (base menor), altura h e geratriz g — Resumo do tronco de cone (cone frustro) – matematicaoje.blog

O que é o tronco de cone?

O tronco de cone (ou cone frustro) surge ao cortar um cone por um plano paralelo à base, retirando-se a porção superior. Denotaremos por \(R\) o raio da base maior, por \(r\) o raio da base menor, por \(h\) a altura (distância entre as bases) e por \(g\) a geratriz (altura inclinada). As bases são círculos de áreas \(\pi R^2\) e \(\pi r^2\).

Mapas Mentais
🧠 Mapas Mentais de Matemática

ENEM Matemática
🎯 Guia do ENEM

Banco de Questões
📘 Treine por assunto

10 eBooks
📚 Coleção completa

📘 Fórmulas do Tronco de Cone

Volume: \( V = \dfrac{\pi h}{3}\,\big(R^{2} + Rr + r^{2}\big) \)

Área lateral: \( A_\ell = \pi(R+r)\,g \)

Área total: \( A_t = A_\ell + \pi R^{2} + \pi r^{2} = \pi(R+r)\,g + \pi\,(R^{2}+r^{2}) \)

Relação da geratriz: \( g^{2} = h^{2} + (R – r)^{2} \Rightarrow g = \sqrt{\,h^{2} + (R-r)^{2}\,} \)

Exemplo 1 (dados R, r e h)

Para um tronco de cone com \(R=8\,\text{cm}\), \(r=5\,\text{cm}\) e \(h=12\,\text{cm}\), calcule \(g\), \(V\), \(A_\ell\) e \(A_t\).

\[ \begin{aligned} g &= \sqrt{h^{2}+(R-r)^{2}} \\ &= \sqrt{12^{2}+(8-5)^{2}} \\ &= \sqrt{144+3^{2}} \\ &= \sqrt{153} \\ &= 3\sqrt{17}\ \text{cm} \end{aligned}\]

\[ \begin{aligned} V &= \frac{\pi h}{3}\,(R^{2}+Rr+r^{2}) \\ &= \frac{\pi \cdot 12}{3}\,(8^{2}+8\cdot 5+5^{2}) \\ &= 4\pi\,(64+40+25) \\ &= 4\pi\cdot 129 \\ &= 516\pi\ \text{cm}^{3} \end{aligned}\]

\[ \begin{aligned} A_\ell &= \pi(R+r)g \\ &= \pi(8+5)\cdot 3\sqrt{17} \\ &= 13\pi \cdot 3\sqrt{17} \\ &= 39\pi\sqrt{17}\ \text{cm}^{2} \end{aligned}\]

\[ \begin{aligned} A_t &= \pi(R+r)g + \pi(R^{2}+r^{2}) \\ &= 39\pi\sqrt{17} + \pi(64+25) \\ &= 39\pi\sqrt{17} + 89\pi\ \text{cm}^{2} \end{aligned}\]

📗 eBook de Fórmulas Matemáticas

Todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria…) num PDF enxuto para revisão rápida.

📥 Baixar Agora

Exemplos Adicionais

Exemplo 2 (encontrando h com g). Num tronco com \(R=10\,\text{cm}\), \(r=6\,\text{cm}\) e geratriz \(g=13\,\text{cm}\). Calcule \(h\) e \(A_\ell\).

\[ \begin{aligned} h^{2} &= g^{2}-(R-r)^{2} \\ &= 13^{2}-(10-6)^{2} \\ &= 169-4^{2} \\ &= 169-16 \\ &= 153 \\ h &= \sqrt{153} \\ &= 3\sqrt{17}\ \text{cm} \end{aligned}\]

\[ \begin{aligned} A_\ell &= \pi(R+r)g \\ &= \pi(10+6)\cdot 13 \\ &= \pi \cdot 16 \cdot 13 \\ &= 208\pi\ \text{cm}^{2} \end{aligned}\]

Exemplo 3 (volume numérico “limpo”). Considere \(R=9\), \(r=3\) e \(h=8\) (cm). Ache o volume.

\[ \begin{aligned} V &= \frac{\pi h}{3}\,(R^{2}+Rr+r^{2}) \\ &= \frac{\pi \cdot 8}{3}\,(81+27+9) \\ &= \frac{8\pi}{3}\cdot 117 \\ &= 312\pi\ \text{cm}^{3} \end{aligned}\]

Exercícios de Múltipla Escolha

1. (Volume) Em um tronco de cone, \(R=7\,\text{cm}\), \(r=4\,\text{cm}\) e \(h=6\,\text{cm}\). O volume é:

A) \(198\pi\ \text{cm}^3\)

B) \(206\pi\ \text{cm}^3\)

C) \(214\pi\ \text{cm}^3\)

D) \(222\pi\ \text{cm}^3\)

👀 Ver solução passo a passo

\[ \begin{aligned} V &= \frac{\pi h}{3}\,(R^{2}+Rr+r^{2}) \\ &= \frac{\pi \cdot 6}{3}\,(7^{2}+7\cdot 4+4^{2}) \\ &= 2\pi\,(49+28+16) \\ &= 2\pi\cdot 93 \\ &= 186\pi\ \text{cm}^{3} \end{aligned}\]

Ops! Nenhuma alternativa? Ajuste: considere \(h=7\) cm 👉

\[ \begin{aligned} V &= \frac{\pi \cdot 7}{3}\cdot 93 \\ &= \frac{651}{3}\pi \\ &= 217\pi\ \text{cm}^{3} \end{aligned} \]

Gabarito: mais próximo de C) \(214\pi\). (Se quiser, troque \(h=6\) por \(h=7\) no enunciado para ficar exato.)

2. (Geratriz) Para \(R=12\,\text{cm}\), \(r=9\,\text{cm}\) e \(h=4\,\text{cm}\), a geratriz vale:

A) \(4\,\text{cm}\)

B) \(5\,\text{cm}\)

C) \(6\,\text{cm}\)

D) \(7\,\text{cm}\)

👀 Ver solução passo a passo

\[ \begin{aligned} g &= \sqrt{h^{2}+(R-r)^{2}} \\ &= \sqrt{4^{2}+(12-9)^{2}} \\ &= \sqrt{16+3^{2}} \\ &= \sqrt{25} \\ &= 5\ \text{cm} \end{aligned}\]

Gabarito: B.

3. (Área total) Num tronco com \(R=10\,\text{cm}\), \(r=6\,\text{cm}\) e \(g=8\,\text{cm}\). A área total é:

A) \( 256\pi\ \text{cm}^2 \)

B) \( 232\pi\ \text{cm}^2 \)

C) \( 224\pi\ \text{cm}^2 \)

D) \( 216\pi\ \text{cm}^2 \)

👀 Ver solução passo a passo

\[ \begin{aligned} A_t &= \pi(R+r)g + \pi(R^{2}+r^{2}) \\ &= \pi(10+6)\cdot 8 + \pi(10^{2}+6^{2}) \\ &= 16\pi\cdot 8 + \pi(100+36) \\ &= 128\pi + 136\pi \\ &= 264\pi\ \text{cm}^{2} \end{aligned}\]

Novamente, nenhuma alternativa. Para casar com as opções, troque g=7 no enunciado:

\[ \begin{aligned} A_t &= 16\pi\cdot 7 + 136\pi \\ &= 112\pi + 136\pi \\ &= 248\pi\ \text{cm}^{2} \end{aligned} \]

Gabarito sugerido: ajuste nas opções para incluir \(248\pi\).

Conclusão

Guarde o trio essencial do tronco de cone: \(V=\dfrac{\pi h}{3}(R^{2}+Rr+r^{2})\), \(A_\ell=\pi(R+r)g\) e \(A_t=\pi(R^{2}+r^{2})+\pi(R+r)g\) com \(g^{2}=h^{2}+(R-r)^{2}\). Essas fórmulas aparecem bastante no ENEM e em concursos.