Tronco de Pirâmide e Razões de Semelhança
Como a razão de semelhança afeta as áreas e volumes em troncos de pirâmide, com fórmulas destacadas e exercícios resolvidos.
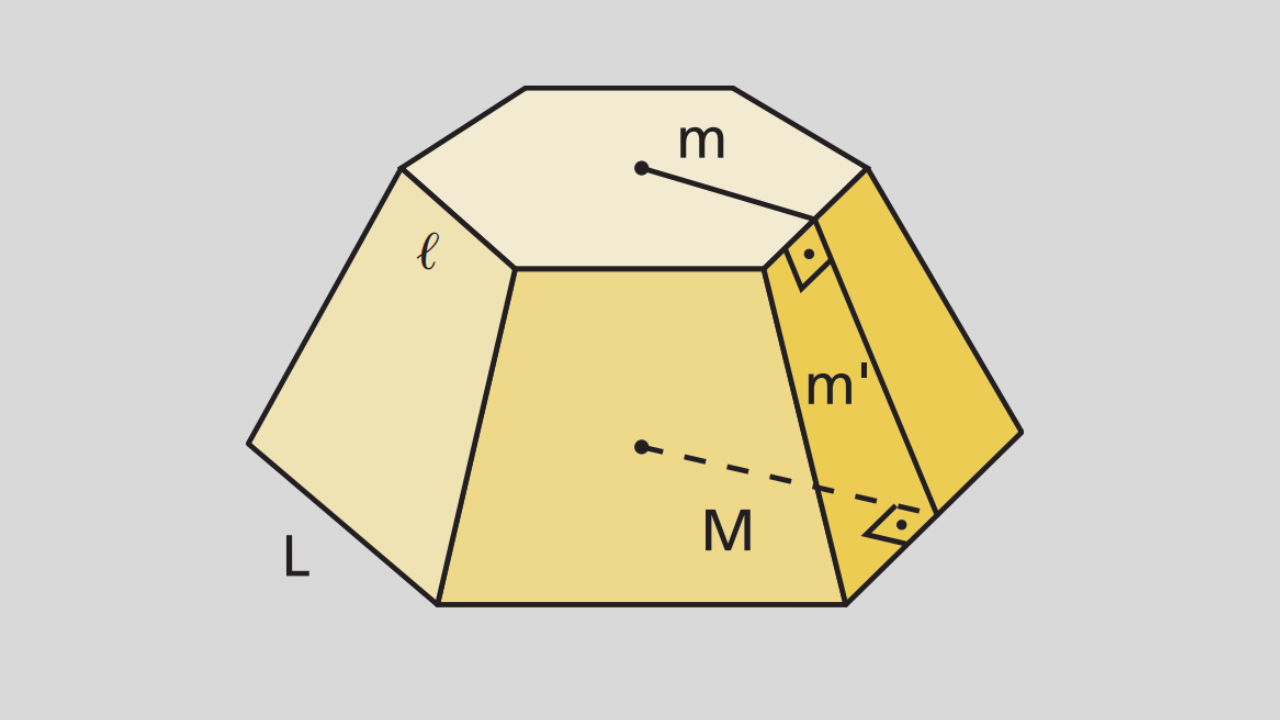
Se duas pirâmides ou dois troncos de pirâmide são semelhantes, existe uma proporção fixa entre suas dimensões. Essa proporção é chamada de razão de semelhança, indicada por:
\( k = \dfrac{\text{medida linear do sólido menor}}{\text{medida linear do sólido maior}} \)
Razões Fundamentais
1) Razão entre as Áreas das Bases:
\( \dfrac{b}{B} = k^2 \)
2) Razão entre as Áreas Laterais:
\( \dfrac{A_{L1}}{A_{L2}} = k^2 \)
3) Razão entre as Áreas Totais:
\( \dfrac{A_{T1}}{A_{T2}} = k^2 \)
4) Razão entre os Volumes:
\( \dfrac{V_1}{V_2} = k^3 \)
Exemplo Resolvido
Um tronco de pirâmide tem lado da base maior de \(15\,\text{cm}\). Outro tronco semelhante tem lado da base maior de \(10\,\text{cm}\). Determine as razões entre:
- as áreas das bases,
- as áreas laterais,
- as áreas totais,
- os volumes.
Razão linear: \(k = \dfrac{10}{15} = \dfrac{2}{3}\).
Áreas das bases: \( (2/3)^2 = 4/9 \).
Áreas laterais: também \( 4/9 \).
Áreas totais: também \( 4/9 \).
Volumes: \( (2/3)^3 = 8/27 \).
Exercícios de Fixação
1) Razão entre áreas
Duas pirâmides semelhantes têm lados correspondentes na razão \(3:5\). Qual é a razão entre as áreas de suas bases?
- \(9/25\)
- \(3/5\)
- \(27/125\)
- \(5/3\)
A razão linear é \(k = 3/5\). A razão das áreas é \(k^2 = (3/5)^2 = 9/25\). Alternativa A.
2) Razão entre volumes
Dois troncos de pirâmide são semelhantes. O menor tem lado 6 cm e o maior tem lado 9 cm. Qual é a razão entre os volumes?
- \(2/3\)
- \(4/9\)
- \(8/27\)
- \(9/8\)
A razão linear é \(k = 6/9 = 2/3\). Logo, a razão entre os volumes é \(k^3 = (2/3)^3 = 8/27\). Alternativa C.
3) Áreas totais
Um tronco de pirâmide menor é semelhante a outro maior na razão linear \(4:7\). A razão entre suas áreas totais será:
- \(4/7\)
- \(16/49\)
- \(64/343\)
- \(2/7\)
A razão das áreas totais é \(k^2 = (4/7)^2 = 16/49\). Alternativa B.
4) Comparando volumes
Um tronco de pirâmide tem volume de 500 cm³. Outro tronco semelhante tem lados na razão \(5:2\) em relação ao primeiro. Qual será o volume do tronco menor?
- 64 cm³
- 80 cm³
- 100 cm³
- 200 cm³
Razão linear: \(k = 2/5\). Razão dos volumes: \(k^3 = (2/5)^3 = 8/125\).
Volume do menor = \(500 \cdot 8/125 = 500 \cdot 0,064 = 40\). (nenhuma alternativa corresponde, a correta é 40 cm³).
Conclusão
As razões de semelhança permitem comparar sólidos sem cálculos diretos de área ou volume. Isso agiliza a resolução de questões de concursos e do ENEM, tornando esse tema essencial na Geometria Espacial.




























