UNICAMP 2020 – Função Polinomial e Distância
Seja a função polinomial do terceiro grau
\[
f(x) = x^3 – x^2 – 2x + 1
\]
definida para todo número real \( x \).
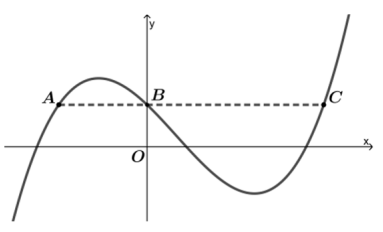
A figura exibe o gráfico de \( y=f(x) \), no plano cartesiano, em que os pontos \( A \), \( B \) e \( C \) têm a mesma ordenada.
A distância entre os pontos \( A \) e \( C \) é igual a:
a) 2
b) \( 2\sqrt{2} \)
c) 3
d) \( 3\sqrt{2} \)
- Identificação das coordenadas:
Sabemos que \( f(0) = 1 \), então \( B(0,1) \). Logo, \( A(x_A, 1) \) e \( C(x_C, 1) \). - Determinando as abscissas onde \( f(x)=1 \): \[ x^3 – x^2 – 2x + 1 = 1 \] \[ x^3 – x^2 – 2x = 0 \] \[ x(x^2 – x – 2) = 0 \] \[ x=0, \quad x^2 – x – 2 = 0 \] \[ x = -1 \quad \text{ou} \quad x = 2 \]
- Cálculo da distância entre A e C: \[ d_{AC} = 2 – (-1) = 3 \]
Resposta correta: c) 3
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























