UNICAMP 2021 – Funções Polinomiais de 2º Grau
Sejam \( p(x) \) e \( q(x) \) polinômios de grau 2 tais que \( p(0) < q(0) \).
Sabendo que \( p(1) = q(1) \) e \( p(-1) = q(-1) \), o gráfico de
\( f(x) = p(x) – q(x) \) pode ser representado por:
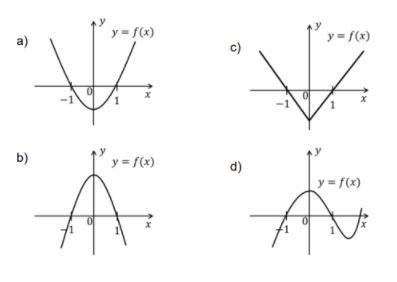
- Seja \( p(x) = ax^2 + bx + c \) e \( q(x) = mx^2 + nx + p \), com \( a \neq 0 \) e \( m \neq 0 \).
- De \( p(0) < q(0) \) temos \( c – p < 0 \).
- De \( p(1) = q(1) \) temos \( a + b + c = m + n + p \).
- De \( p(-1) = q(-1) \) temos \( a – b + c = m – n + p \).
- Somando as duas últimas: \( 2a + 2c = 2m + 2p \Rightarrow a + c = m + p \Rightarrow a – m = p – c \).
- Subtraindo: \( 2b = 2n \Rightarrow b = n \).
- Logo, \( f(x) = p(x) – q(x) = (a-m)x^2 + (b-n)x + (c-p) \).
Com \( a-m > 0 \), \( b-n = 0 \), \( c-p < 0 \), trata-se de uma parábola voltada para cima. - Verificando as raízes: \( x = \pm 1 \) são zeros de \( f(x) \).
- Portanto, o gráfico correto é a alternativa A.
