UNICAMP 2021 – Questão de Sequência de Polígonos
Sejam \( a, b \) números reais positivos. Considere a sequência de polígonos \( P_1, P_2, \dots, P_n, \dots \) construída da seguinte forma:
1. \( P_1 \) é um retângulo de lados \( a \) e \( b \); 2. \( P_2 \) é obtido de \( P_1 \), retirando um retângulo de lados \( a/2 \) e \( b/2 \); 3. \( P_3 \) é obtido de \( P_1 \), retirando 3 retângulos de lados \( a/3 \) e \( b/3 \); 4. \( P_4 \) é obtido de \( P_1 \), retirando 6 retângulos de lados \( a/4 \) e \( b/4 \); 5. E assim sucessivamente, \( P_n \) é obtido de \( P_1 \) como mostrado na figura.
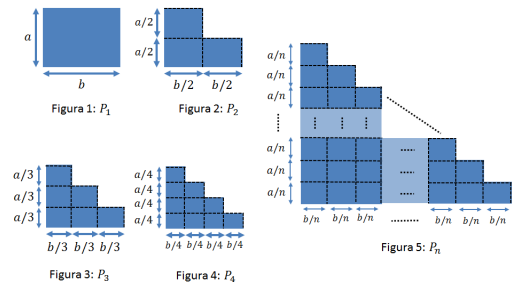
a) Determine o perímetro e o número de lados de \( P_{2021} \). b) Seja \( A_n \) a área do polígono \( P_n \) e \( A \) a área do triângulo retângulo de catetos \( a \) e \( b \). Encontre a razão \( R_n = \frac{A_n}{A} \) para \( n \) arbitrário.
1. \( P_1 \) é um retângulo de lados \( a \) e \( b \); 2. \( P_2 \) é obtido de \( P_1 \), retirando um retângulo de lados \( a/2 \) e \( b/2 \); 3. \( P_3 \) é obtido de \( P_1 \), retirando 3 retângulos de lados \( a/3 \) e \( b/3 \); 4. \( P_4 \) é obtido de \( P_1 \), retirando 6 retângulos de lados \( a/4 \) e \( b/4 \); 5. E assim sucessivamente, \( P_n \) é obtido de \( P_1 \) como mostrado na figura.
a) Determine o perímetro e o número de lados de \( P_{2021} \). b) Seja \( A_n \) a área do polígono \( P_n \) e \( A \) a área do triângulo retângulo de catetos \( a \) e \( b \). Encontre a razão \( R_n = \frac{A_n}{A} \) para \( n \) arbitrário.
- Perímetro e número de lados de \( P_{2021} \):
- O perímetro de qualquer \( P_n \) permanece igual ao retângulo inicial: \[ 2a + 2b \]
- O número de lados cresce de 2 em 2 a cada etapa: \[ L_n = 2n + 2 \]
- Para \( n = 2021 \): \[ L_{2021} = 2 \cdot 2021 + 2 = 4044 \]
- Razão de áreas \( R_n \):
- Número de retângulos em \( P_n \): \[ 1 + 2 + \dots + n = \frac{n(n+1)}{2} \]
- Área de cada retângulo: \[ \frac{a}{n} \cdot \frac{b}{n} = \frac{ab}{n^2} \]
- Área do polígono: \[ A_n = \frac{n(n+1)}{2} \cdot \frac{ab}{n^2} = \frac{(n+1)ab}{2n} \]
- Área do triângulo retângulo de catetos \( a \) e \( b \): \[ A = \frac{ab}{2} \]
- Razão entre as áreas: \[ R_n = \frac{A_n}{A} = \frac{(n+1)/n}{1} = 1 + \frac{1}{n} \]
Respostas finais:
- \( P_{2021} \) possui perímetro \( 2a + 2b \) e \( 4044 \) lados.
- \( R_n = 1 + \frac{1}{n} \).
