UNICAMP 2022 | Matemática | Aplicação de Trigonometria
No dia 23 de março de 2021, um navio encalhou no canal de Suez, no Egito. A embarcação tinha 400 metros de comprimento e 60 metros de largura. No ponto onde aconteceu o acidente, o canal de Suez não tem mais do que 200 metros de largura. O ângulo indicado na figura mede \(67,5^\circ\).
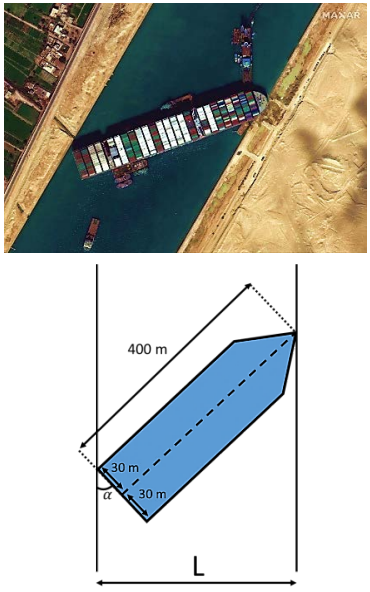
A largura do canal \(L\), em metros, é aproximadamente:
a) \( 400\sqrt{2-\sqrt{2}} – 60\sqrt{2+\sqrt{2}} \approx 195,3 \)
b) \( 200\sqrt{2-\sqrt{2}} – 15\sqrt{2+\sqrt{2}} \approx 125,4 \)
c) \( 200\sqrt{2-\sqrt{2}} + 15\sqrt{2+\sqrt{2}} \approx 180,8 \)
d) \( 200\sqrt{3-\sqrt{3}} – 15\sqrt{3+\sqrt{3}} \approx 192,6 \)
Resolução Passo a Passo:
1) Usando identidades trigonométricas:
\[
\cos(2\alpha) = 2\cos^2\alpha – 1
\quad\Rightarrow\quad
\cos\alpha = \sqrt{\frac{\cos 2\alpha + 1}{2}}
\]
\[
sen\alpha = \sqrt{\frac{1-\cos 2\alpha}{2}}
\]Para \(\alpha = 67,5^\circ\):
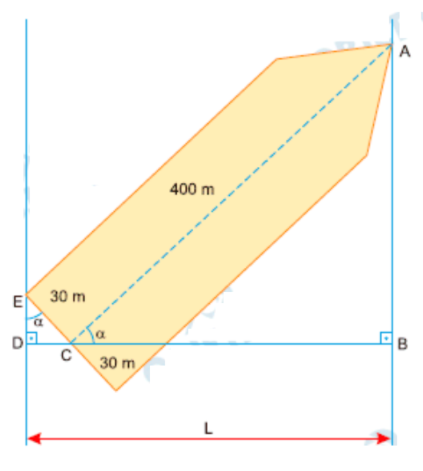
\[ \cos\alpha = \frac{\sqrt{2-\sqrt{2}}}{2}, \quad sen\alpha = \frac{\sqrt{2+\sqrt{2}}}{2} \]2) Considerando os triângulos retângulos formados pelo navio:
\[ L = 400 \cdot \cos\alpha + 30 \cdot sen\alpha \] \[ L = 200\sqrt{2-\sqrt{2}} + 15\sqrt{2+\sqrt{2}} \approx 180,8 \text{ m} \]Resposta: c) 180,8 metros
