UNICAMP 2022 | Matemática | Quadrilátero Tangencial e Progressão Aritmética
Um círculo está inscrito em um quadrilátero \(ABCD\). Seja \(T\) o ponto de tangência do lado \(DA\) com o círculo. Sabe-se que as medidas dos lados \(AB\), \(BC\) e \(CD\) formam, nesta ordem, uma progressão aritmética crescente de números inteiros e que a medida do lado \(DA\) é 3. Considerando que a medida do segmento \(TA\) é um número inteiro, as medidas dos lados \(AB\), \(BC\) e \(CD\) são, respectivamente:
a) 1, 3, 5
b) 2, 3, 4
c) 2, 4, 6
d) 3, 4, 5
Resolução:
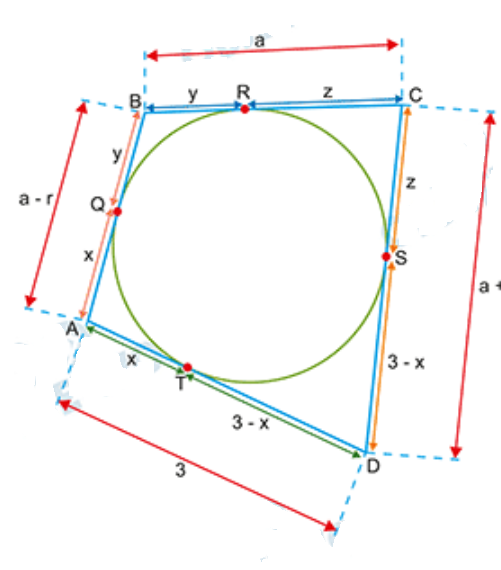
1) Denotando os lados como: \[ AB = a-r, \quad BC = a, \quad CD = a+r \] com \( r > 0 \), pois formam uma progressão aritmética.
2) Pela tangência do círculo: \[ x+y = a-r, \quad y+z = a, \quad z+3-x = a+r \] Subtraindo as equações, obtemos: \[ 0 = a-3 \Rightarrow a = 3 \]
3) Como \( AB = a-r \) é inteiro positivo, \( r=1 \): \[ AB = 2, \quad BC = 3, \quad CD = 4 \]
Resposta: b) 2, 3, 4📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























