A figura mostra um triângulo retângulo ABC. O ponto \( M \) é o ponto médio do lado \( AB \), que é a hipotenusa.
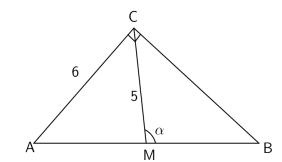
O valor de \( sen \alpha \) é:
-
a) \( \frac{24}{25} \)
b) \( \frac{5}{6} \)
c) \( \frac{1}{2} \)
d) \( \frac{\sqrt{3}}{2} \)
I) Identificando o ponto M:
O ponto \( M \) é o circuncentro do triângulo retângulo \( ABC \), pois é o ponto médio da hipotenusa. Assim, \( AM = BM = CM = 5 \), logo: \[ AB = AM + MB = 5 + 5 = 10 \]
II) Determinando os lados do triângulo:
No triângulo \( ABC \): \[ (BC)^2 + (AC)^2 = (AB)^2 \] \[ (BC)^2 + 6^2 = 10^2 \Rightarrow BC^2 = 64 \Rightarrow BC = 8 \] \[ sen B = \frac{AC}{AB} = \frac{6}{10} = \frac{3}{5} \]
III) Aplicando a lei dos senos no triângulo BMC:
\[ \frac{CM}{sen B} = \frac{BC}{sen \alpha} \] \[ \frac{5}{3/5} = \frac{8}{sen \alpha} \Rightarrow sen \alpha = \frac{24}{25} \]
Resposta Final: Alternativa A.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























