A seguir, são apresentadas quatro funções, definidas para \(x \in \mathbb{R}\), e são também apresentados quatro esboços de gráficos.
Funções:
\( f(x) = sen\left(x + \frac{\pi}{4}\right) \)
\( g(x) = \cos\left(x + \frac{\pi}{4}\right) – sen\left(x + \frac{\pi}{4}\right) \)
\( h(x) = sen\left(x – \frac{\pi}{4}\right) \)
\( p(x) = \cos x + sen x \)
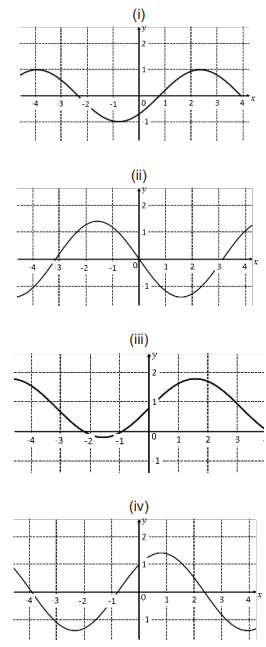
Os esboços dos gráficos são numerados como:
(i), (ii), (iii), (iv)
A opção que descreve corretamente a correspondência entre as funções e seus gráficos é:
-
a) (i) g(x); (ii) h(x); (iii) p(x); (iv) f(x)
b) (i) h(x); (ii) g(x); (iii) f(x); (iv) p(x)
c) (i) p(x); (ii) g(x); (iii) h(x); (iv) f(x)
d) (i) f(x); (ii) p(x); (iii) g(x); (iv) h(x)
1) Analisando a função \(f(x) = sen\left(x+\frac{\pi}{4}\right)\):
O gráfico é uma translação da função seno para a esquerda em \(\frac{\pi}{4}\). Comparando com os esboços fornecidos, identificamos que corresponde ao **gráfico (iv)**.
2) Função \(g(x) = \cos(x+\frac{\pi}{4}) – sen(x+\frac{\pi}{4})\):
Podemos reescrever \(g(x) = \sqrt{2}sen\left(x+\frac{\pi}{4}-\frac{\pi}{2}\right) = -\sqrt{2}sen x\). Observando os gráficos, identificamos que corresponde ao **gráfico (ii)**.
3) Função \(h(x) = sen\left(x-\frac{\pi}{4}\right)\):
É uma translação da função seno para a direita em \(\frac{\pi}{4}\), correspondendo ao **gráfico (i)**.
4) Função \(p(x) = \cos x + sen x\):
Pode ser escrita como \(p(x)=\sqrt{2}sen\left(x+\frac{\pi}{4}\right)\), que tem amplitude \(\sqrt{2}\) e corresponde ao **gráfico (iii)**.
Assim, a correspondência correta é: (i) h(x); (ii) g(x); (iii) f(x); (iv) p(x) Resposta: Alternativa B.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: