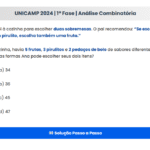
Três números reais distintos \(a, b, c\) são tais que \(a, b, c\) e \(ab, bc, ca\) formam, nessa ordem, duas progressões aritméticas de mesma razão. O valor do produto \(abc\) é:
-
a) 1
b) 1/8
c) -1
d) 6
1) Considerando a PA (a; b; c):
\( a – b = r \quad\text{e}\quad c = b + r \)
2) Substituindo na PA (ab; bc; ca):
\((b-r)\cdot b,\quad b\cdot(b+r),\quad (b+r)(b-r)\) ou seja: \( (b^2 – rb),\; b^2 + rb,\; b^2 – r^2 \)
3) Da razão da PA:
\( (b^2+rb) – (b^2-rb) = 2rb \) \( 2rb = r^2 + rb \Rightarrow r \neq 0 \Rightarrow b = \frac{1}{2} \)
4) Substituindo em a e c:
\(a = b – r = \frac{1}{2} – \frac{3}{2} = -1\) \(b = \frac{1}{2}\) \(c = b + r = 2\)
5) Produto final:
\( abc = (-1)\cdot \frac{1}{2} \cdot 2 = -1 \)
Resposta Final: Alternativa C.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: