Um recipiente cilíndrico de altura \(h\) tem água em seu interior. Ao mergulhar uma esfera de chumbo de raio \(R\) neste recipiente, a água cobre a esfera e nenhuma quantidade de água se perde, como ilustrado na figura a seguir.
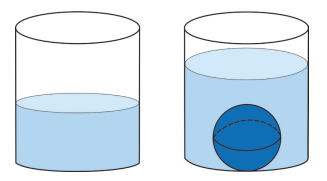
Sabendo que o raio da base do cilindro é o dobro do raio da esfera, a diferença entre a altura da água antes e depois do mergulho da esfera é igual a:
-
a) 2R
b) R
c) R/3
d) 2R/3
1) Relação entre volumes:
O volume da esfera de raio \(R\) é: \[ V_{\text{esfera}} = \frac{4}{3}\pi R^3 \]
O volume do cilindro que corresponde à variação de altura \(h\) da água tem raio \(2R\) e altura \(h\): \[ V_{\text{cilindro}} = \pi (2R)^2 \cdot h = 4\pi R^2 h \]
2) Igualando os volumes deslocados:
\[ \frac{4}{3}\pi R^3 = 4 \pi R^2 \cdot h \]
Simplificando: \[ \frac{R}{3} = h \]
3) Conclusão:
A diferença na altura da água é R/3. Resposta: C.
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:

























