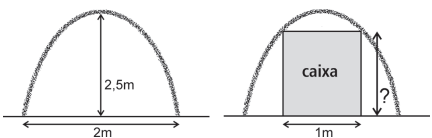
Laura é geóloga e está fazendo pesquisas em uma caverna cuja entrada tem o formato de uma parábola invertida. Essa entrada tem 2 metros de largura e o ponto mais alto está a 2,5 metros do chão.
Laura precisa entrar com um equipamento em uma caixa de 1 metro de largura. Qual é a altura máxima, em metros, que a caixa pode ter para passar pela entrada da caverna?
-
a) 11/8
b) 13/8
c) 15/8
d) 17/8
1) Determinando o vértice:
A parábola tem zeros em \( x = 0 \) e \( x = 2 \). O vértice está em: \[ x_v = \frac{0+2}{2} = 1 \]
2) Forma fatorada da parábola:
\[ f(x) = a \cdot x (x-2) \]
3) Encontrando o coeficiente \( a \):
Usando o ponto máximo \( (1, \frac{5}{2}) \): \[ \frac{5}{2} = a \cdot 1 \cdot (1-2) \implies a = -\frac{5}{2} \]
4) Altura máxima da caixa de 1 m:
Metade da largura de 1 m para cada lado do vértice: \[ f\left(\frac{1}{2}\right) = -\frac{5}{2} \cdot \frac{1}{2} \cdot \left(\frac{1}{2}-2\right) = \frac{15}{8} \]
Resposta Final: **Alternativa c) 15/8 metros**
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:




























