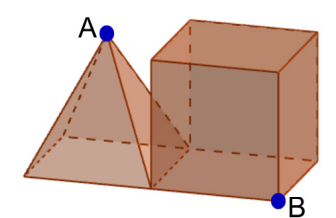
A figura abaixo mostra uma pirâmide e um cubo, que compartilham uma aresta da base da pirâmide. A pirâmide tem altura de 1 m e base quadrada de 1 m de lado. O cubo também possui arestas de 1 m.
a) Um sólido é formado pela união desses dois objetos. Qual é o seu volume?
b) Determine a distância do ponto A (vértice superior da pirâmide) até o ponto B (vértice frontal da base do cubo que não está na aresta em comum com a pirâmide).
a) Volume do sólido
O volume do sólido é a soma do volume do cubo com o da pirâmide: \[ V = 1^3 + \frac{1}{3} \cdot 1^2 \cdot 1 = \frac{4}{3} \text{ m}^3 \]
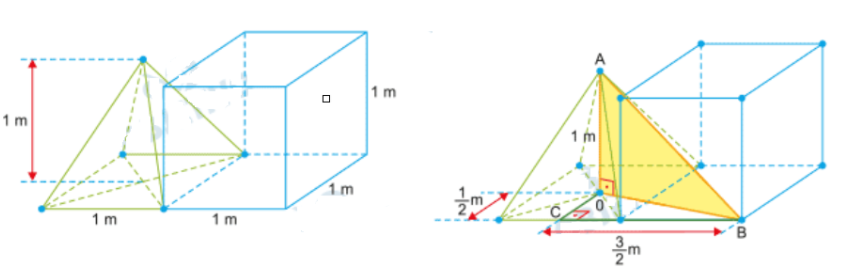
b) Distância de A até B
Considerando a projeção ortogonal:
- No triângulo retângulo \( CBO \): \[ OB^2 = \left(\frac{1}{2}\right)^2 + \left(\frac{3}{2}\right)^2 = \frac{10}{4} \]
- No triângulo retângulo \( OBA \): \[ AB^2 = AO^2 + OB^2 = 1^2 + \frac{10}{4} = \frac{14}{4} \]
Logo: \[ AB = \frac{\sqrt{14}}{2} \text{ m} \]
Resposta Final: a) \( \frac{4}{3} \, \text{m}^3 \) b) \( \frac{\sqrt{14}}{2} \, \text{m} \)
