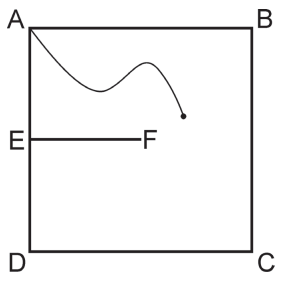
Na figura abaixo, \(ABCD\) representa um terreno quadrado com lados de 10 m, coberto por grama alta. O ponto \(E\) é o ponto médio do lado \(AD\); o segmento \(EF\), paralelo a \(DC\), representa um muro de 5 m de comprimento e 1 m de altura, portanto, intransponível.
Um cortador de grama robótico será usado para cortar a grama do terreno. Ele será ligado na energia no ponto \(A\) e seu cabo de energia tem comprimento de 10 m. Para funcionar, ele precisa estar ligado o tempo todo.
-
a) Ao usar o aparelho para cortar a grama do terreno, uma pessoa tenta se aproximar, ao máximo, do lado \(CD\).
Calcule a distância que falta para o cortador alcançar o lado \(CD\).
b) O robô não conseguirá cortar todo o terreno, pois seu fio é curto e o muro é obstáculo.
Determine a maior área do terreno que o robô conseguirá cortar.
a) Distância faltante para alcançar o lado CD
Primeiro, calculamos \( AF \) no triângulo retângulo: \[ AF^2 = 5^2 + 5^2 \implies AF = 5\sqrt{2} \]
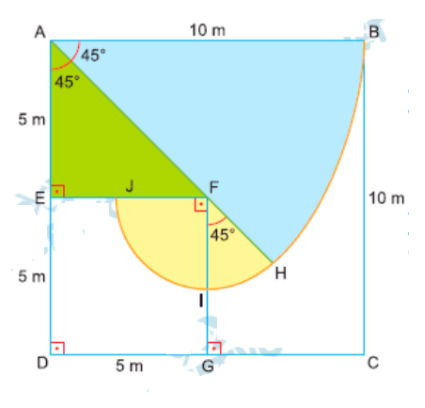
O cabo tem 10 m, logo o ponto mais próximo que o robô chega do lado \(CD\) está a: \[ GI = 5\sqrt{2} – 10 \approx 1 \text{ m de distância} \]
b) Maior área que o robô consegue cortar
A área acessível é composta por setores circulares com raio 10 m, descontando o setor bloqueado pelo muro: \[ A = \frac{45^\circ}{360^\circ} \pi \cdot 10^2 + \frac{135^\circ}{360^\circ} \pi \cdot (10-5\sqrt{2})^2 + 5 \cdot 5 \]
Simplificando: \[ A = \frac{550\pi – 300\pi \sqrt{2} + 100}{8} = \frac{275\pi – 150\pi\sqrt{2} + 50}{4} \text{ m²} \]
Resposta Final: a) \(5\sqrt{2} – 10 \approx 1 \text{ m}\) b) \(\frac{275\pi – 150\pi\sqrt{2} + 50}{4} \text{ m²}\)
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo: