UNICAMP 2024 | 2ª Fase | Geometria Analítica e Interseção de Conjuntos
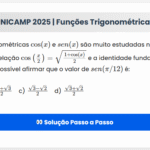
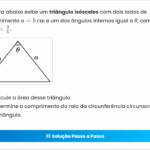
Considere os conjuntos: \[ A = \{(x,y) \in \mathbb{R}^2 \mid 2 \le y \le \frac{x}{2}+1 \} \] \[ B = \{(x,y) \in \mathbb{R}^2 \mid y \le -\frac{x}{4} + \frac{13}{4} \} \]
- O ponto \( \left(\frac{3}{2}, 1\right) \) está em \( A \cap B \)? E o ponto \( \left(3, \frac{12}{5}\right) \)? Justifique.
- Calcule a área de \( A \cap B \).
a) Verificação de pontos na interseção
A interseção das retas que delimitam \( A \) e \( B \) ocorre na solução do sistema: \[ \begin{cases} y = \frac{x}{2}+1 \\ y = -\frac{x}{4}+\frac{13}{4} \end{cases} \implies x=3 \]
- Para \( \left(\frac{3}{2}, 1\right) \): \(y = 1 < 2\), logo **não pertence** a \( A \cap B \).
- Para \( \left(3, \frac{12}{5}\right) \): \(2 \le \frac{12}{5} \le 2,5\), logo **pertence** a \( A \cap B \).
b) Cálculo da área da interseção
A interseção \( A \cap B \) forma um triângulo de base 3 e altura \( \frac{5}{2}-2 = \frac{1}{2} \): \[ A = \frac{3 \cdot \frac{1}{2}}{2} = \frac{3}{4} \]
Resposta Final: a) \( \left(\frac{3}{2}, 1\right) \notin A \cap B \) e \( \left(3, \frac{12}{5}\right) \in A \cap B \) b) Área = \( \frac{3}{4} \)
Relacionadas
