Uma escola tem 4 turmas: A, B, C e D. As turmas B e C têm, cada uma delas, uma quantidade \( x \) de alunos, e as turmas A e D têm, cada uma delas, uma quantidade \( 3x \) de alunos.
Em determinado momento do ano, foi realizada uma eleição para o Grêmio Estudantil, e havia duas candidaturas: Chapa 1 e Chapa 2. O gráfico abaixo mostra o resultado da votação, em percentual, em cada uma das turmas. Sabe-se que todos os alunos votaram, e não houve nenhum voto branco ou nulo.
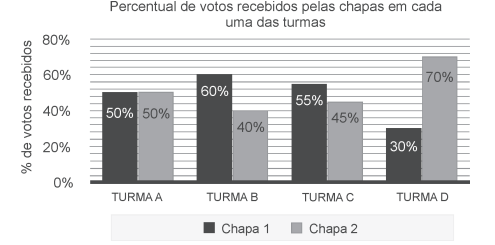
Há duas propostas sobre como definir a chapa vencedora da eleição:
- Proposta 1: vence a eleição a chapa que receber a maior quantidade de votos, considerando o total de votos da escola.
- Proposta 2: vence a eleição a chapa que ficar em primeiro lugar no maior número de salas (isto é, receber mais votos em mais turmas).
a) Qual chapa seria vencedora se fosse adotada a Proposta 1? Haverá alguma mudança se a Proposta 2 for adotada? Justifique suas respostas.
b) Sabendo que a escola tem 160 alunos, informe, na tabela disposta, quantos alunos cada uma das turmas tem e justifique sua resposta.
1) Quantidade de votos de cada chapa:
Para cada turma:
- Chapa 1: \( 0,5 \cdot 3x + 0,55x + 0,3x + 0,55x = 3,55x \)
- Chapa 2: \( 0,5 \cdot 3x + 0,4x + 0,45x + 0,7x = 4,45x \)
Pela Proposta 1, a vencedora é a Chapa 2 pois \( 4,45x > 3,55x \).
Pela Proposta 2, a vencedora é a Chapa 1 pois venceu em duas turmas e empatou em uma.
2) Cálculo da quantidade de alunos por turma:
\[ 3x + x + x + 3x = 8x = 160 \implies x = 20 \]
| Turma | A | B | C | D |
|---|---|---|---|---|
| Quantidade de alunos | 60 | 20 | 20 | 60 |
Resposta Final: – Proposta 1 → **Chapa 2** – Proposta 2 → **Chapa 1** – Quantidade de alunos por turma: A = 60, B = 20, C = 20, D = 60
📘 Questões MATEMÁTICA UNICAMP Resolvidas
Escolha o ano e acesse as questões com solução passo a passo:













