Rayssa participou dos Jogos Olímpicos de Paris. Ela visitou quatro pontos turísticos: o Arco do Triunfo, a Catedral de Notre-Dame, o Museu do Louvre e a Torre Eiffel.
a) Rayssa escolheu a melhor foto que tirou de cada um desses pontos turísticos e publicará uma por dia em suas redes sociais, ao longo de quatro dias consecutivos, sem repetir nenhuma foto. De quantas maneiras ela pode fazer isso?
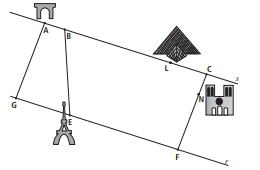
b) A figura abaixo mostra os pontos turísticos e as ruas de Paris que conectam esses pontos. As retas \( r \) e \( s \) são paralelas e os segmentos \( AG \) e \( CF \) são paralelos entre si e perpendiculares a \( r \) e \( s \). Considerando as distâncias em km apresentadas no enunciado, calcule a **menor distância possível** que Rayssa percorreu ao visitar os pontos na ordem: Arco do Triunfo → Torre Eiffel → Catedral de Notre-Dame → Museu do Louvre.
a) Número de maneiras de postar as fotos:
Temos 4 fotos distintas e 4 dias → permutação simples: \[ 4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24 \]
b) Menor distância percorrida:
1) No triângulo retângulo \( EBH \), pelo Teorema de Pitágoras: \[ EH^2 + 0,8^2 = 1,7^2 \] \[ EH \approx 1,5 \text{ km} \]
2) Soma das menores distâncias: \[ A \to E: 0,5 + 1,7 = 2,2 \text{ km} \] \[ E \to N: 2,7 + (1,5-0,5) = 3,7 \text{ km} \] \[ N \to L: 0,5 + 1 = 1,5 \text{ km} \]
**Distância total:** \[ 2,2 + 3,7 + 1,5 = 7,4 \text{ km} \]
Resposta Final: a) 24 b) 7,4 km
