Questões que envolvem função quadrática e interpretação de gráficos aparecem com frequência na UNICAMP, especialmente em situações aplicadas à Física e ao esporte. Nesta questão, analisamos a trajetória parabólica da bola em um jogo de vôlei, utilizando informações de altura, distância e ponto de máximo da parábola.
🔗 Dando continuidade à sequência de resoluções: Questão 47 – Escala e Área
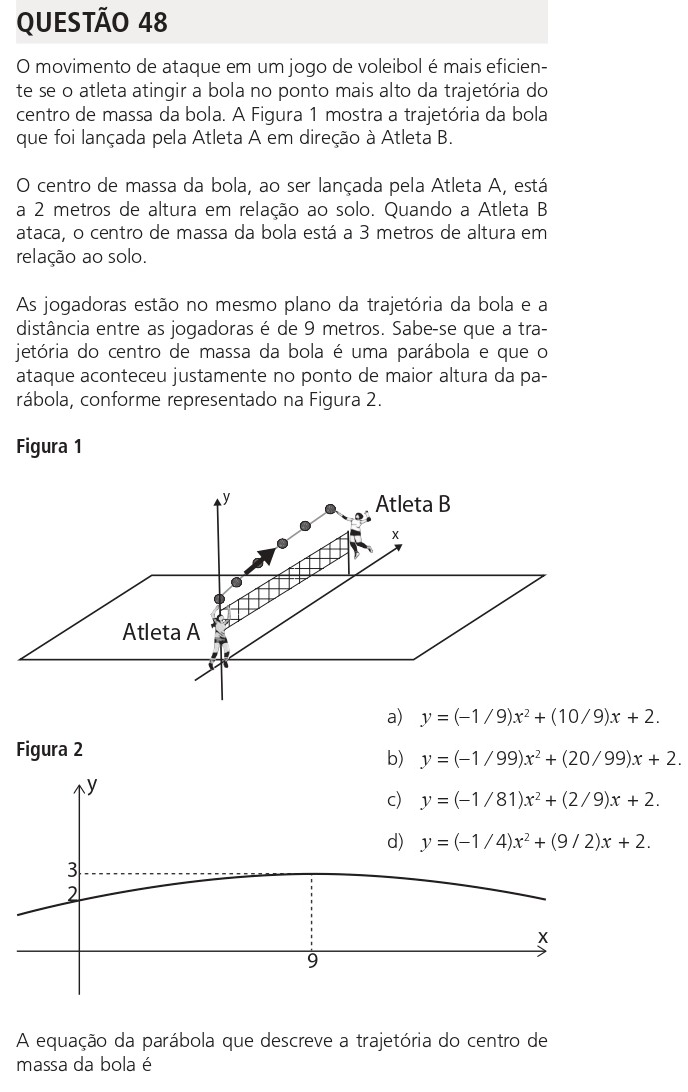
Descrição da imagem: gráfico da parábola representando a trajetória da bola, com vértice em x = 9 e y = 3.
✅ Clique aqui para ver a solução passo a passo
1) Identificando os dados do problema
A bola:
• Parte da altura 2 m → ponto (0, 2)
• Atinge o ponto máximo no ataque → vértice da parábola
• Altura máxima: 3 m
• Distância horizontal entre as atletas: 9 m
Logo, o vértice da parábola é:
V = (9, 3)
2) Forma canônica da função quadrática
A equação da parábola pode ser escrita na forma:
y = a(x − 9)² + 3
3) Usando o ponto inicial da trajetória
Sabemos que a bola passa pelo ponto:
(0, 2)
Substituindo:
2 = a(0 − 9)² + 3
2 = 81a + 3
81a = −1
a = −1/81
4) Obtendo a equação da parábola
y = (−1/81)(x − 9)² + 3
Desenvolvendo:
y = (−1/81)(x² − 18x + 81) + 3
y = −(1/81)x² + (18/81)x − 1 + 3
y = −(1/81)x² + (2/9)x + 2
✅ Resposta correta: alternativa C













