Esta questão da UNICAMP 2026 trabalha com Geometria Plana em um quadrado, explorando a localização de pontos sobre os lados e o cálculo da área de uma região sombreada. A ideia é traduzir a figura para um sistema de coordenadas, encontrar o ponto de interseção de segmentos e, por fim, calcular a área de um triângulo usando base e altura.
🔗 Dando continuidade à sequência: Questão 52 – Sistema de Equações Lineares
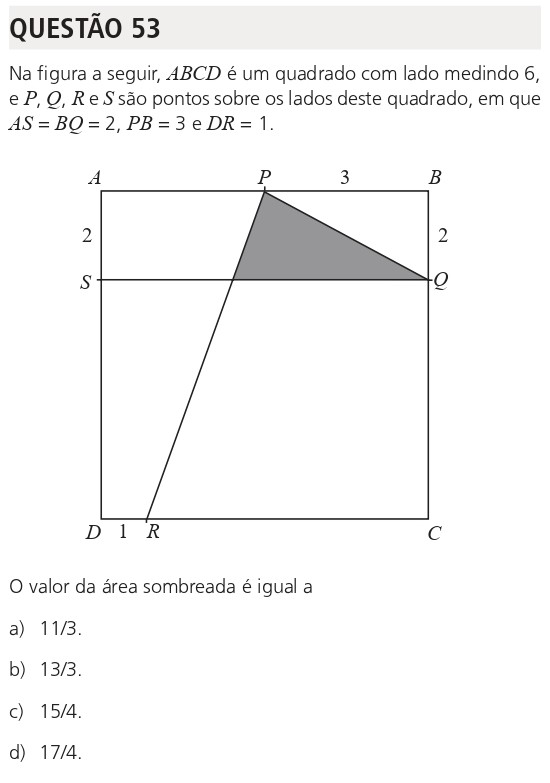
Descrição da imagem: quadrado de lado 6 com pontos marcados nos lados e região sombreada próxima ao topo.
✅ Clique aqui para ver a solução passo a passo
1) Montando um sistema de coordenadas
Considere o quadrado ABCD com lado 6 e posicione-o no plano cartesiano:
D = (0, 0), C = (6, 0), B = (6, 6), A = (0, 6).
Do enunciado:
• AS = 2 ⟹ S está 2 unidades abaixo de A, logo S = (0, 4).
• BQ = 2 ⟹ Q está 2 unidades abaixo de B, logo Q = (6, 4).
• PB = 3 e AB = 6 ⟹ P está a 3 unidades de B sobre AB, logo P = (3, 6).
• DR = 1 ⟹ R está a 1 unidade de D sobre DC, logo R = (1, 0).
A região sombreada é o triângulo formado pelos pontos P, Q e T, em que T é a interseção do segmento PR com o segmento horizontal SQ.
2) Encontrando a interseção T entre PR e SQ
A reta PR passa por P(3, 6) e R(1, 0).
Coeficiente angular:
m = (0 − 6) / (1 − 3) = −6 / −2 = 3
Equação de PR:
y − 6 = 3(x − 3) ⟹ y = 3x − 3
O segmento SQ é horizontal, com y = 4.
Para achar T, fazemos:
4 = 3x − 3
3x = 7
x = 7/3
Logo:
T = (7/3, 4)
3) Área do triângulo PTQ
O triângulo sombreado tem vértices P(3, 6), T(7/3, 4) e Q(6, 4).
A base pode ser o segmento TQ, que é horizontal (mesma altura y = 4):
TQ = 6 − 7/3 = (18 − 7)/3 = 11/3
A altura correspondente é a distância vertical de P até a reta y = 4:
h = 6 − 4 = 2
Área do triângulo:
A = (base · altura) / 2
A = ( (11/3) · 2 ) / 2
A = 11/3
✅ Resposta correta: alternativa A = 11/3













