Valor máximo e mínimo de uma função quadrática

Valor máximo e mínimo de uma função quadrática (f(x)=ax²+bx+c)

Valor máximo e mínimo de uma função quadrática

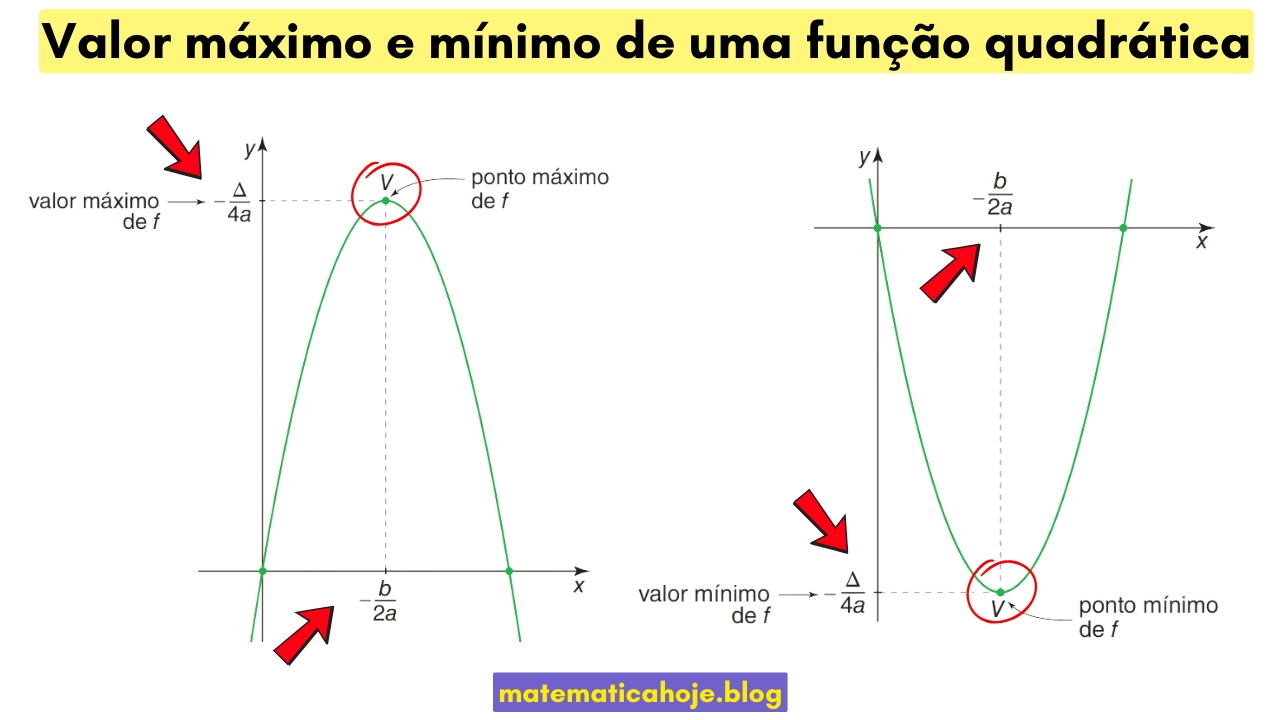
Para $f(x)=ax^2+bx+c$ com $a\neq 0$, o ponto de máximo/mínimo é o vértice $V(x_v,y_v)$. O tipo (máximo ou mínimo) depende apenas do sinal de $a$:

Concavidade

$a>0$ ⟶ parábola abre para cima ⟶ valor mínimo.
$a<0$ ⟶ parábola abre para baixo ⟶ valor máximo.

Fórmulas do vértice

\[ x_v=-\frac{b}{2a},\qquad y_v=-\frac{\Delta}{4a},\quad \text{onde}\ \Delta=b^2-4ac. \]

Equivalente pela forma canônica $f(x)=a(x-h)^2+k$: $h=x_v$ e $k=y_v$.

$Parábolas mostrando que com a<0 há valor máximo e com a>0 há valor mínimo; yv = -Δ/(4a) e xv = -b/(2a).”><h2>Como calcular em 3 passos</h2><ol><li>Identifique $a,b,c$.</li><li>Calcule $x_v=-\dfrac{b}{2a}$.</li><li>Calcule $y_v$ usando $y_v=-\dfrac{\Delta}{4a}$ ou $y_v=f(x_v)$.</li></ol><section class=$

📘 E-book: Fórmulas de Matemática (referência rápida e completa)

Tenha à mão todas as fórmulas de função quadrática, equações, inequações e muito mais. Ótimo para revisões rápidas e preparação para provas.

Acessar o E-book de Fórmulas

Exemplos resolvidos (com contas uma embaixo da outra)

Exemplo 1 — Valor máximo

Para $f(x)=-2x^2+4x+6$, encontre o valor máximo e o ponto onde ocorre.

\[ \begin{aligned} a&=-2,\ b=4,\ c=6\\[2pt] x_v&=-\frac{b}{2a}\\ &=-\frac{4}{2(-2)}\\ &=-\frac{4}{-4}\\ &=1\\[6pt] y_v&=f(1)\\ &=-2(1)^2+4(1)+6\\ &=-2+4+6\\ &=8 \end{aligned} \]

Como $a<0$, $y_v=8$ é o valor máximo e ocorre em $x=1$.

Exemplo 2 — Valor mínimo

Para $g(x)=3x^2-6x+2$, determine o valor mínimo.

\[ \begin{aligned} a&=3,\ b=-6,\ c=2\\[2pt] x_v&=-\frac{b}{2a}\\ &=-\frac{-6}{2\cdot 3}\\ &=\frac{6}{6}\\ &=1\\[6pt] y_v&=g(1)\\ &=3(1)^2-6(1)+2\\ &=3-6+2\\ &=-1 \end{aligned} \]

Como $a>0$, $y_v=-1$ é o valor mínimo, em $x=1$.

Exemplo 3 — Sem raízes reais, mas com mínimo

Para $h(x)=x^2+2x+5$, calcule o mínimo.

\[ \begin{aligned} a&=1,\ b=2,\ c=5\\[2pt] \Delta&=b^2-4ac\\ &=2^2-4(1)(5)\\ &=4-20\\ &=-16\\[6pt] y_v&=-\frac{\Delta}{4a}\\ &=-\frac{-16}{4\cdot 1}\\ &=\frac{16}{4}\\ &=4\\[6pt] x_v&=-\frac{b}{2a}\\ &=-\frac{2}{2}\\ &=-1 \end{aligned} \]

$\Delta<0$ (sem zeros), mas $a>0$ garante mínimo $=4$ em $x=-1$.

Aplicação típica (otimização)

Receita máxima: $R(x)=-2x^2+120x$. Qual $x$ maximiza $R$ e qual é a receita máxima?

\[ \begin{aligned} a&=-2,\ b=120\\[2pt] x_v&=-\frac{b}{2a}\\ &=-\frac{120}{2(-2)}\\ &=-\frac{120}{-4}\\ &=30\\[6pt] R_{\max}&=R(30)\\ &=-2(30)^2+120(30)\\ &=-2\cdot 900+3600\\ &=-1800+3600\\ &=1800 \end{aligned} \]

Receita máxima de R$ 1.800 ocorre para $x=30$ unidades.

Exercícios propostos

1) Encontre o valor máximo de $f(x)=-x^2+8x-5$ e o ponto onde ocorre.

Gabarito

\[ \begin{aligned} a&=-1,\ b=8,\ c=-5\\ x_v&=-\frac{8}{2(-1)}=4\\ y_v&=f(4)\\ &=-(4)^2+8(4)-5\\ &=-16+32-5\\ &=11 \end{aligned} \]

Máximo $=11$ em $x=4$.

2) Determine o mínimo de $g(x)=2x^2+4x+1$.

Gabarito

\[ \begin{aligned} a&=2,\ b=4,\ c=1\\ x_v&=-\frac{4}{2\cdot 2}=-1\\ y_v&=g(-1)\\ &=2(1)+4(-1)+1\\ &=2-4+1\\ &=-1 \end{aligned} \]

Mínimo $-1$ em $x=-1$.

3) Para $h(x)=x^2-10x+c$, encontre $c$ tal que o valor mínimo seja $9$.

Gabarito

\[ \begin{aligned} a&=1,\ b=-10\\ x_v&=-\frac{-10}{2\cdot 1}=5\\ h_{\min}&=h(5)=9\\ 9&=(5)^2-10(5)+c\\ &=25-50+c\\ 9&=-25+c\\ c&=34 \end{aligned} \]

Logo $c=34$.

Continue aprendendo (links internos)

Função Quadrática (guia completo) Gráfico da função quadrática Coeficiente $a$: concavidade e abertura Coeficientes $b$ e $c$: eixo e intercepto Pontos notáveis da parábola Foco e diretriz da parábola

Materiais recomendados (produtos do blog)

Mapas Mentais de Matemática Preparação ENEM Matemática Coleção com 10 E-books Banco de Questões de Matemática E-book de Fórmulas (referência rápida)

Relacionadas

Soma e Produto das Raízes da Equação do 2º Grau

Função Quadrática: o papel do coeficiente a

Função Quadrática

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.