Valor mínimo e valor máximo da função quadrática
Ao esboçarmos o gráfico de uma função quadrática \( f(x) = ax^2 + bx + c \), podemos usar o sinal do coeficiente \( a \) para identificar se a concavidade da parábola é voltada para cima ou para baixo.
Se a > 0, a concavidade da parábola é voltada para cima, e o vértice representa o valor mínimo. Veja os exemplos:
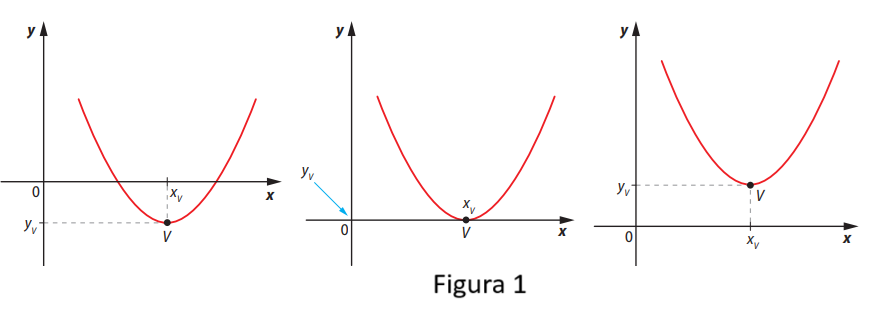
Se a < 0, a concavidade da parábola é voltada para baixo, e o vértice representa o valor máximo. Veja os exemplos:
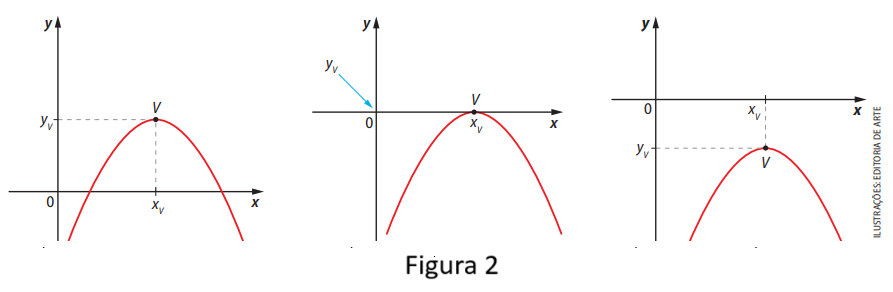
A ordenada do vértice é o valor máximo ou mínimo da função, calculada por:
\[ y_v = \frac{-\Delta}{4a} \quad \text{com} \quad \Delta = b^2 – 4ac \]
Exemplo aplicado
Considere a função do lucro diário de uma loja de capas para celular:
\[ L(x) = -x^2 + 55x – 250 \]
Essa função atinge o valor máximo no vértice. Vamos calcular:
\[ x_v = \frac{-b}{2a} = \frac{-55}{2(-1)} = \frac{55}{2} = 27{,}5 \]
Logo, o lucro máximo é obtido quando o preço da capa é R$ 27,50.
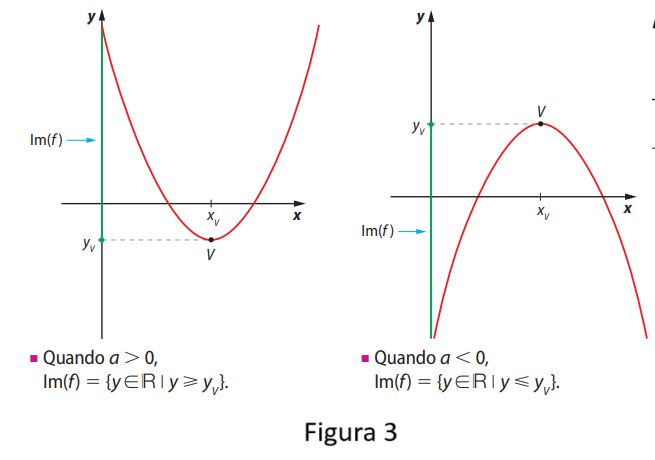
Imagem da função quadrática
A imagem da função quadrática corresponde ao conjunto de todos os valores possíveis de \( y \).
- Se \( a > 0 \): a imagem é \([y_v, +\infty[\)
- Se \( a < 0 \): a imagem é \(]-\infty, y_v]\)
Exercício 1. Determine o valor mínimo da função \( f(x) = 2x^2 – 8x + 6 \).
👀 Ver solução
1. Identificando os coeficientes: a = 2, b = -8, c = 6
2. Abscissa do vértice:
$$ x_v = \frac{-b}{2a} = \frac{-(-8)}{2 \cdot 2} = \frac{8}{4} = 2 $$
3. Ordenada do vértice:
$$ y_v = f(2) = 2(2)^2 – 8(2) + 6 = 8 – 16 + 6 = -2 $$
Resposta: Valor mínimo = −2
Exercício 2. Uma empresa modela o lucro com \( L(x) = -x^2 + 10x \). Qual número de unidades produzidas por dia gera o lucro máximo?
👀 Ver solução
1. Coeficientes: a = -1, b = 10
2. Abscissa do vértice:
$$ x_v = \frac{-10}{2 \cdot (-1)} = \frac{-10}{-2} = 5 $$
Resposta: 5 unidades
Exercício 3. A função \( f(x) = -3x^2 + 12x – 7 \) representa a trajetória de um projétil. Qual é a altura máxima atingida?
👀 Ver solução
1. Coeficientes: a = -3, b = 12, c = -7
2. Abscissa do vértice:
$$ x_v = \frac{-12}{2 \cdot (-3)} = 2 $$
3. Ordenada do vértice:
$$ y_v = -3(2)^2 + 12(2) – 7 = -12 + 24 – 7 = 5 $$
Altura máxima: 5 metros
Exercício 4. Qual o valor mínimo da função \( f(x) = x^2 + 4x + 9 \)?
👀 Ver solução
1. Coeficientes: a = 1, b = 4, c = 9
2. Abscissa do vértice:
$$ x_v = \frac{-4}{2 \cdot 1} = -2 $$
3. Ordenada do vértice:
$$ y_v = (-2)^2 + 4(-2) + 9 = 4 – 8 + 9 = 5 $$
Resposta: Valor mínimo = 5






















