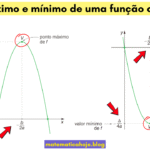
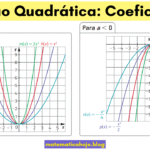
Variação de sinal da função quadrática (estudo de sinal completo)
Para \(f(x)=ax^2+bx+c\,(a\ne 0)\), queremos saber onde \(f(x)>0\), \(f(x)<0\) ou \(f(x)=0\). A resposta depende do sinal de \(a\) (concavidade) e do número de raízes reais, dado por \(\Delta=b^2-4ac\).

- Se \(a>0\) (parábola para cima):
• \(\Delta>0\): \(f(x)>0\) para \(x<x_1\) ou \(x>x_2\); \(f(x)<0\) para \(x_1<x<x_2\); \(f(x)=0\) em \(x_1,x_2\). • \(\Delta=0\): \(f(x)\ge 0\) para todo \(x\) e \(f(x)=0\) apenas no vértice \(x_1=x_2\). • \(\Delta<0\): \(f(x)>0\) para todo \(x\) (não zera).
- Se \(a<0\) (parábola para baixo):
• \(\Delta>0\): \(f(x)<0\) para \(x<x_1\) ou \(x>x_2\); \(f(x)>0\) para \(x_1<x<x_2\); \(f(x)=0\) em \(x_1,x_2\). • \(\Delta=0\): \(f(x)\le 0\) para todo \(x\) e \(f(x)=0\) apenas no vértice \(x_1=x_2\). • \(\Delta<0\): \(f(x)<0\) para todo \(x\) (não zera).
Como decidir o sinal (passo a passo)
1) Calcule \(\Delta=b^2-4ac\).
2) Se \(\Delta>0\), ache \(x_1\) e \(x_2\) pela fórmula de Bhaskara e ordene \(x_1<x_2\).
3) Observe o sinal de \(a\) e use o resumo acima para concluir onde \(f(x)\) é +, − ou 0.
Exemplos resolvidos (contas em coluna)
Exemplo 1 — \(f(x)=x^2-5x+4\) (a>0, Δ>0)
Objetivo: decidir onde \(f\) é positiva, negativa e nula.
Delta e raízes
\(\Delta=b^2-4ac\)
\(=(-5)^2-4\cdot 1\cdot 4\)
\(=25-16\)
\(=9\)
\(x=\dfrac{-b\pm\sqrt{\Delta}}{2a}\)
\(=\dfrac{5\pm 3}{2}\)
\(x_1=1,\; x_2=4\)
Sinal (a>0)
\(f(x)>0\) se \(x<1\) ou \(x>4\).
\(f(x)<0\) se \(1<x<4\).
\(f(x)=0\) em \(x=1\) e \(x=4\).
Exemplo 2 — \(g(x)=-2x^2+6x-4\) (a<0, Δ=0)
Objetivo: classificar o sinal no \(\mathbb{R}\).
Delta e raiz dupla
\(\Delta=b^2-4ac\)
\(=6^2-4\cdot(-2)\cdot(-4)\)
\(=36-32\)
\(=4\)
\(x=\dfrac{-b\pm\sqrt{\Delta}}{2a}=\dfrac{-6\pm 2}{-4}\Rightarrow x_1=x_2=\dfrac{3}{2}\)
Sinal (a<0, Δ=0)
\(g(x)\le 0\) para todo \(x\) e \(g(x)=0\) apenas em \(x=\dfrac{3}{2}\).
Exemplo 3 — \(h(x)=2x^2+3x+5\) (a>0, Δ<0)
Objetivo: decidir o sinal global.
Delta
\(\Delta=3^2-4\cdot 2\cdot 5\)
\(=9-40\)
\(=-31\lt 0\)
Sinal (a>0, Δ<0)
Sem raízes reais e concavidade para cima ⇒ \(h(x)>0\) para todo \(x\).
Exemplo 4 — \(p(x)=-x^2-4x-8\) (a<0, Δ<0)
Objetivo: decidir o sinal global.
Delta
\(\Delta=(-4)^2-4\cdot(-1)\cdot(-8)\)
\(=16-32\)
\(=-16\lt 0\)
Sinal (a<0, Δ<0)
Sem raízes reais e concavidade para baixo ⇒ \(p(x)<0\) para todo \(x\).
Dicas rápidas
- Fatoração ajuda no Δ>0: se \(f(x)=a(x-x_1)(x-x_2)\), o sinal muda ao atravessar cada raiz simples.
- Raiz dupla (Δ=0) não troca sinal: toca o eixo \(x\) no vértice e volta.
- Olhe primeiro para \(a\): já diz o “lado” do sinal fora do intervalo entre as raízes.
Links internos para revisar
Quer um atalho nas provas? Consulte o eBook de Fórmulas de Matemática com Bhaskara, vértice, relações úteis e muito mais — perfeito para revisão de última hora.