Vértice da Parábola — Fórmulas, Coordenadas e Significado

O vértice da parábola resume o comportamento da função do segundo grau: indica máximo (se $a<0$) ou mínimo (se $a>0$).

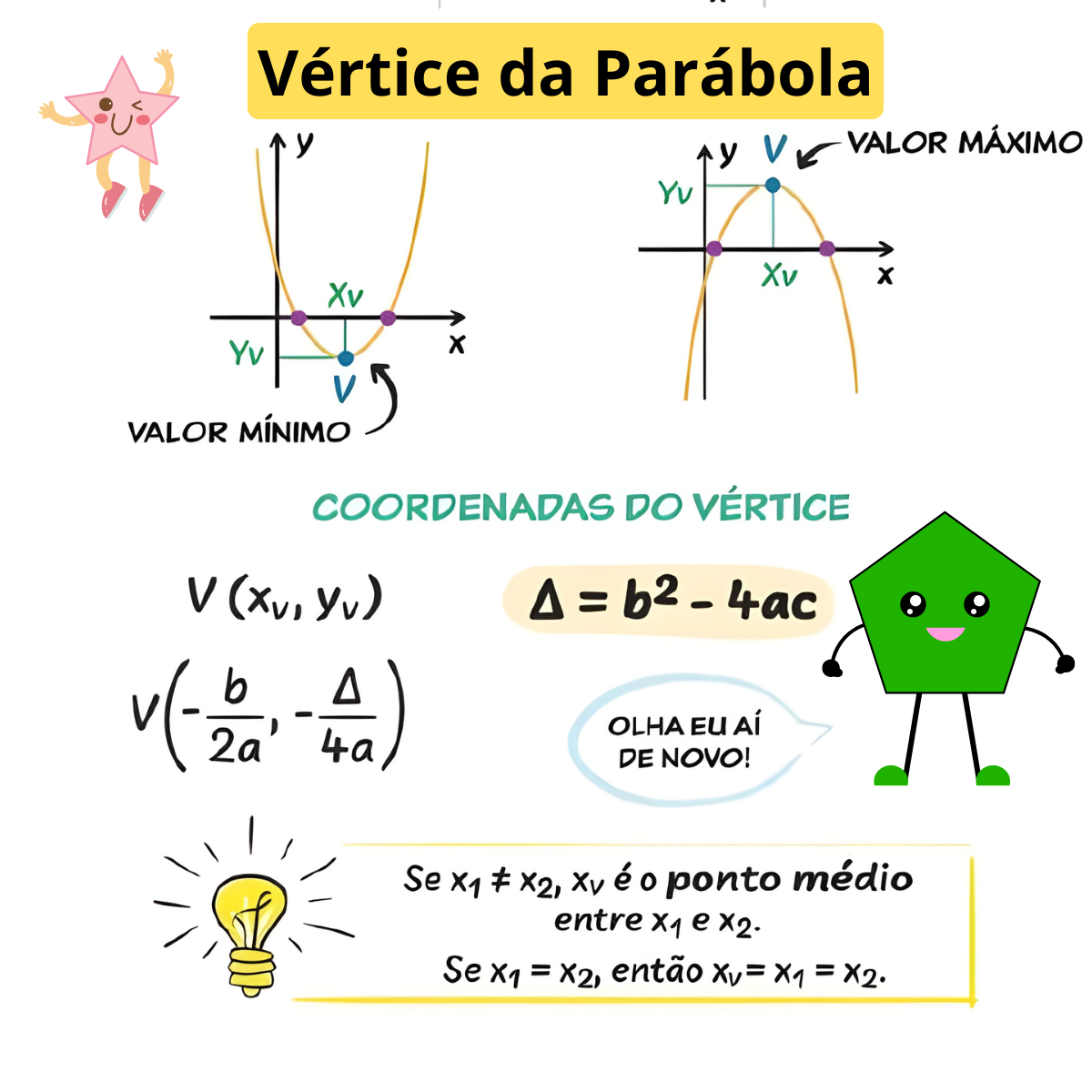
Vértice da parábola: valor máximo e mínimo, fórmulas e interpretação.

📐 Fórmulas essenciais

Para $ f(x)=ax^2+bx+c $ (com $a\neq0$):

$$ V(x_v,y_v)=\left(-\frac{b}{2a}, -\frac{\Delta}{4a}\right), \quad \Delta=b^2-4ac. $$

Além disso, se as raízes $x_1$ e $x_2$ existem, então $x_v$ é o ponto médio: $$ x_v=\frac{x_1+x_2}{2}. $$

💡 Baixe o eBook de Fórmulas Matemática (PDF)
Todas as fórmulas em um só lugar para ENEM e concursos.

Exemplo rápido

Para $f(x)=x^2-4x+3$:

$x_v=-\dfrac{b}{2a}=-\dfrac{-4}{2\cdot1}= \dfrac{4}{2}=2$
$y_v=f(2)=(2)^2-4\cdot2+3=4-8+3=-1$
$\Rightarrow V(2,-1)$ (mínimo, pois $a>0$).

📝 Exercícios — Vértice da Parábola

Inclui questões abertas e múltipla escolha com soluções em “abre/fecha”.

1) (Múltipla escolha) Para $f(x)=ax^2+bx+c$, o vértice representa um valor máximo quando:

A) $a>0$ B) $a=0$ C) $a<0$ D) $b<0$

👀 Ver solução

Máximo ocorre quando a parábola é côncava para baixo ⇒ $a<0$. Alternativa C.

2) (Múltipla escolha) Em $f(x)=2x^2-6x+1$, o $x_v$ é:

A) $-\dfrac{6}{4}$ B) $\dfrac{6}{4}$ C) $\dfrac{-6}{2}$ D) $\dfrac{6}{2}$

👀 Ver solução

$x_v=-\dfrac{b}{2a}=-\dfrac{-6}{2\cdot2}=\dfrac{6}{4}=\dfrac{3}{2}$. Alternativa B.

3) Calcule o vértice de $g(x)=-x^2+4x+5$.

👀 Ver solução passo a passo

Identificando: $a=-1$, $b=4$, $c=5$.

$x_v=-\dfrac{b}{2a}=-\dfrac{4}{2\cdot(-1)}=-\dfrac{4}{-2}=2$

$y_v=g(2)=- (2)^2 + 4\cdot2 + 5 = -4 + 8 + 5 = 9$

V(2, 9) (máximo, pois $a<0$).

4) (Múltipla escolha) Em $h(x)=x^2+bx+9$, sabe-se que $x_v= -3$. Qual é o valor de $b$?

A) $-6$ B) $6$ C) $3$ D) $-3$

👀 Ver solução

$x_v=-\dfrac{b}{2a}\Rightarrow -3=-\dfrac{b}{2\cdot1}\Rightarrow -3=-\dfrac{b}{2}$

$\Rightarrow b=6$. Alternativa B.

5) Mostre que, se $x_1$ e $x_2$ são raízes de $f(x)=ax^2+bx+c$, então $x_v=\dfrac{x_1+x_2}{2}$.

👀 Ver solução passo a passo

Pelas relações de Viète: $x_1+x_2=-\dfrac{b}{a}$.

$\dfrac{x_1+x_2}{2}=\dfrac{-b/a}{2}=-\dfrac{b}{2a}=x_v$.

6) (Múltipla escolha) Para $p(x)=3x^2+12x-7$, o $y_v$ é:

A) $-\dfrac{\Delta}{4a}$ B) $\dfrac{\Delta}{4a}$ C) $-\dfrac{b}{2a}$ D) $p(0)$

👀 Ver solução

Por definição: $y_v=-\dfrac{\Delta}{4a}$. Alternativa A.

Se quiser calcular: $\Delta=b^2-4ac=144-4\cdot3\cdot(-7)=144+84=228$. Então $y_v=-\dfrac{228}{4\cdot3}=-\dfrac{228}{12}=-19$.

7) Para $q(x)=2x^2-8x+k$, determine $k$ sabendo que o vértice está em $y_v=-2$.

👀 Ver solução passo a passo

$x_v=-\dfrac{b}{2a}=-\dfrac{-8}{2\cdot2}=\dfrac{8}{4}=2$

$y_v=q(2)=2(2)^2-8(2)+k=2\cdot4-16+k=8-16+k=-8+k$

Como $y_v=-2$: $-8+k=-2 \Rightarrow k=6$.

8) (Múltipla escolha) Em $r(x)=-2x^2+bx+1$, o vértice está à direita do eixo y. Então:

A) $b<0$ B) $b=0$ C) $b>0$ D) impossível saber

👀 Ver solução

Se $x_v>0$, então $-\dfrac{b}{2a}>0$. Como $a=-2<0$, o denominador é negativo; para a fração ser positiva, $b>0$.

Alternativa C.

Gabarito (múltipla escolha): 1) C 2) B 4) B 6) A 8) C

Continue estudando

Compartilhe com a turma e salve este post para revisão! 💙

Vértice da Parábola

Vértice da Parábola — Fórmulas, Coordenadas e Significado

📐 Fórmulas essenciais

Exemplo rápido

📝 Exercícios — Vértice da Parábola

Continue estudando

Equação do Segundo Grau

Zero ou Raiz da Função do Segundo Grau

Função do Segundo Grau

"Artigo escrito por"

Adriano Rocha

Nos ajude compartilhando esse post 😉

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Equação do Segundo Grau