Volume de uma Pirâmide Quadrada Regular — Guia Completo
Use este guia para aprender a calcular o volume \(V\) e a relacionar altura (h), apótema da base (m), apótema da pirâmide (p), aresta lateral (a) e aresta da base (b).
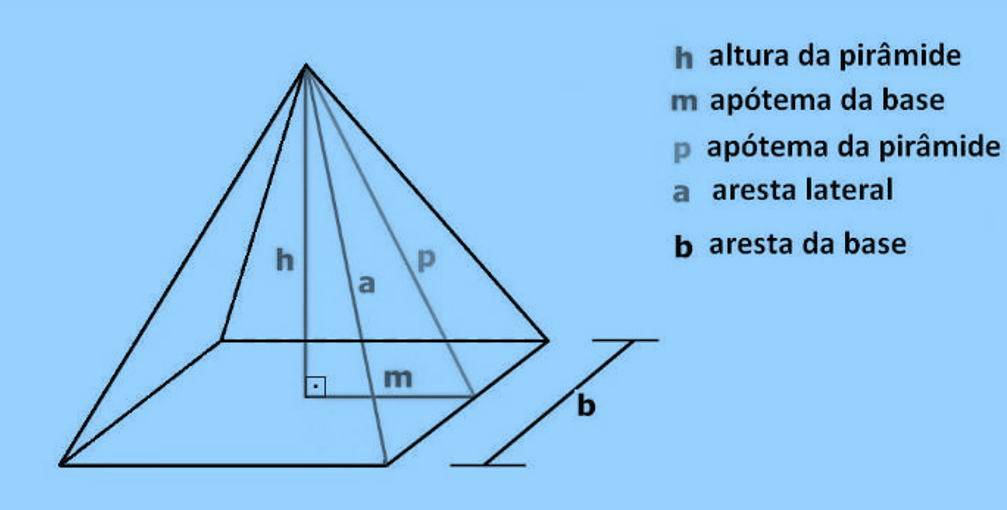
Elementos e notações
- b: aresta (lado) do quadrado da base.
- h: altura da pirâmide (do vértice ao centro da base, perpendicular).
- m: apótema da base — no quadrado é o meio-lado, logo \(m=\tfrac{b}{2}\).
- p: apótema da pirâmide (altura de cada face triangular).
- a: aresta lateral (do vértice até um vértice da base).
Para calcular o volume, basta conhecer \(b\) e \(h\). Se você tiver \(p\) ou \(a\), use as relações geométricas para chegar a \(h\).

Fórmula do volume \(V\)
O volume de qualquer pirâmide é um terço da área da base vezes a altura:
Como a base é um quadrado de lado \(b\), \(B=b^2\). Assim, para a pirâmide quadrada regular:
Se \(b\) e \(h\) estiverem em cm, \(V\) sai em cm³; em metros, sai em m³.
Relações geométricas úteis (conecte com a fórmula)
| Relação | Uso |
|---|---|
| \(m=\dfrac{b}{2}\) | Apótema da base do quadrado. |
| \(p^2=h^2+m^2\) | Triângulo retângulo formado por \(h\) e \(m\) dentro da face ⇒ dá \(h\) a partir de \(p\). |
| \(a^2=h^2+\left(\dfrac{b}{\sqrt{2}}\right)^2=h^2+\dfrac{b^2}{2}\) | Do centro da base ao vértice da base é \( \dfrac{\text{diagonal}}{2}=\dfrac{b\sqrt{2}}{2} \). |
| \(B=b^2\) | Área da base para usar em \(V=\tfrac{1}{3}Bh\). |
Com \(h\) em mãos, volte a \(V=\tfrac{1}{3}b^2h\).
Passo a passo
- Confira quais grandezas possui (\(b,h,p,a\)).
- Se só tiver \(p\) ou \(a\), use as relações para achar \(h\).
- Calcule \(B=b^2\).
- Aplicar \(V=\tfrac{1}{3}b^2h\).
Exemplos resolvidos
Ver solução
Ver solução
Primeiro, \(m=\tfrac{b}{2}=6\). Pelo triângulo retângulo da face: \(h=\sqrt{p^2-m^2}=\sqrt{13^2-6^2}=\sqrt{133}\).
Ver solução
Da relação: \(a^2=h^2+\dfrac{b^2}{2}\Rightarrow h=\sqrt{a^2-\dfrac{b^2}{2}}=\sqrt{100-\dfrac{64}{2}}=\sqrt{100-32}=\sqrt{68}=2\sqrt{17}\).
Exercícios (com solução em abre/fecha)
-
1) Numa pirâmide quadrada regular, \(b=8\text{ m}\) e \(h=15\text{ m}\). Calcule \(V\).
Ver solução
\[ V=\tfrac{1}{3}b^2h=\tfrac{1}{3}\cdot 64\cdot 15=320\ \text{m}^3. \] -
2) Com \(b=10\text{ cm}\) e \(p=13\text{ cm}\), calcule \(V\).
Ver solução
\(m=5\). \(h=\sqrt{p^2-m^2}=\sqrt{169-25}=12\).
\[ V=\tfrac{1}{3}\cdot 100\cdot 12=400\ \text{cm}^3. \] -
3) Uma pirâmide tem \(V=500\ \text{cm}^3\) e \(b=10\ \text{cm}\). Encontre \(h\).
Ver solução
\[ h=\frac{3V}{b^2}=\frac{1500}{100}=15\ \text{cm}. \] -
4) Se \(a=13\text{ cm}\) e \(b=12\text{ cm}\), determine \(h\) e depois \(V\).
Ver solução
\(h=\sqrt{a^2-\dfrac{b^2}{2}}=\sqrt{169-72}= \sqrt{97}\).
\[ V=\tfrac{1}{3}\cdot b^2\cdot h=\tfrac{1}{3}\cdot 144\cdot \sqrt{97}=48\sqrt{97}\ \text{cm}^3. \] -
5) (Contexto) Um objeto decorativo tem \(b=0{,}5\ \text{m}\) e \(h=0{,}24\ \text{m}\). Qual o volume em litros?
Ver solução
\(V=\tfrac{1}{3}\cdot (0{,}5)^2\cdot 0{,}24=0{,}02\ \text{m}^3=20\ \text{L}\).
Se travar em algum exercício, releia o passo a passo e as relações.
FAQ rápido
Posso usar \(V=\tfrac{1}{3}Bh\) para pirâmides não regulares?
Qual a diferença prática entre \(h\) e \(p\)?
Onde entra a imagem no estudo?
Abrir a imagem em nova aba.
Exercícios — Pirâmide Quadrada Regular (múltipla escolha)
Notações: b (aresta da base), h (altura), m (apótema da base), p (apótema da pirâmide), a (aresta lateral). Fórmulas úteis: \(V=\tfrac{1}{3}b^2h\), \(m=\tfrac{b}{2}\), \(p^2=h^2+m^2\), \(a^2=h^2+\tfrac{b^2}{2}\). Consulte a fórmula do volume e as relações geométricas.
-
Monumento urbano. Para um monumento em forma de pirâmide com \(b=10\,\text{m}\) e \(h=18\,\text{m}\), o volume é:
Ver solução
\[V=\tfrac{1}{3}b^2h=\tfrac{1}{3}\cdot100\cdot18=600\ \text{m}^3.\] -
Vitral piramidal. Para um vitral com \(b=6\,\text{m}\) e \(p=5\,\text{m}\), o volume é:
Ver solução
\(m=3\Rightarrow h=\sqrt{5^2-3^2}=4\).
\[V=\tfrac{1}{3}\cdot 36\cdot 4=48\ \text{m}^3.\] -
Montículo de areia. Para uma pirâmide com aresta lateral \(a=13\,\text{m}\) e aresta da base \(b=12\,\text{m}\), o volume é:
Ver solução
\(h=\sqrt{a^2-\tfrac{b^2}{2}}=\sqrt{169-72}=\sqrt{97}\).
\[V=\tfrac{1}{3}\cdot 144\cdot \sqrt{97}=48\sqrt{97}\approx 472{,}75\ \text{m}^3.\] -
Moldagem de concreto. Para um molde com \(V=320\,\text{m}^3\) e \(b=8\,\text{m}\), a altura é:
Ver solução
\[h=\frac{3V}{b^2}=\frac{960}{64}=15\ \text{m}.\] -
Frasco de perfume. Para um frasco piramidal com \(b=5\,\text{cm}\) e \(h=12\,\text{cm}\), a capacidade é:
Ver solução
\[V=\tfrac{1}{3}\cdot25\cdot12=100\ \text{cm}^3=100\ \text{mL}.\] -
Cisterna de irrigação. Uma cisterna com \(b=1{,}0\,\text{m}\) deve armazenar \(2{,}0\,\text{m}^3\). A altura necessária é:
Ver solução
\[h=\frac{3V}{b^2}=3\cdot 2=6\ \text{m}.\] -
Clarabóia. Para \(b=1{,}5\,\text{m}\) e \(p=1{,}3\,\text{m}\), o volume aproximado é:
Ver solução
\(m=0{,}75\Rightarrow h\approx \sqrt{1{,}69-0{,}5625}=1{,}061\).
\[V=\tfrac{1}{3}\cdot(1{,}5)^2\cdot 1{,}061\approx 0{,}796\ \text{m}^3\approx 0{,}80\ \text{m}^3.\] -
Jardim elevado. Para \(b=1{,}2\,\text{m}\) e \(a=1{,}6\,\text{m}\), o volume aproximado é:
Ver solução
\(h\approx \sqrt{2{,}56-0{,}72}=1{,}356\).
\[V=\tfrac{1}{3}\cdot 1{,}44\cdot 1{,}356\approx 0{,}651\ \text{m}^3.\] -
Estande de feira. Dado \(m=0{,}40\,\text{m}\) e \(h=0{,}80\,\text{m}\), o volume é:
Ver solução
\[b=2m=0{,}80\Rightarrow V=\tfrac{1}{3}\cdot 0{,}64\cdot 0{,}80=\tfrac{0{,}512}{3}\approx 0{,}171\ \text{m}^3.\] -
Logística de embalagens. Cada caixa tem \(b=30\,\text{cm}\) e \(h=20\,\text{cm}\). O volume total de 27 caixas é:
Ver solução
Por caixa: \(V=\tfrac{1}{3}(0{,}30)^2(0{,}20)=0{,}006\ \text{m}^3=6\ \text{L}\). Total \(=27\times 6=162\ \text{L}\).













