Volume do Cilindro
O cilindro circular é um dos corpos redondos mais comuns (latas, tubos, reservatórios). Seu volume mede “quanto cabe” dentro do sólido.
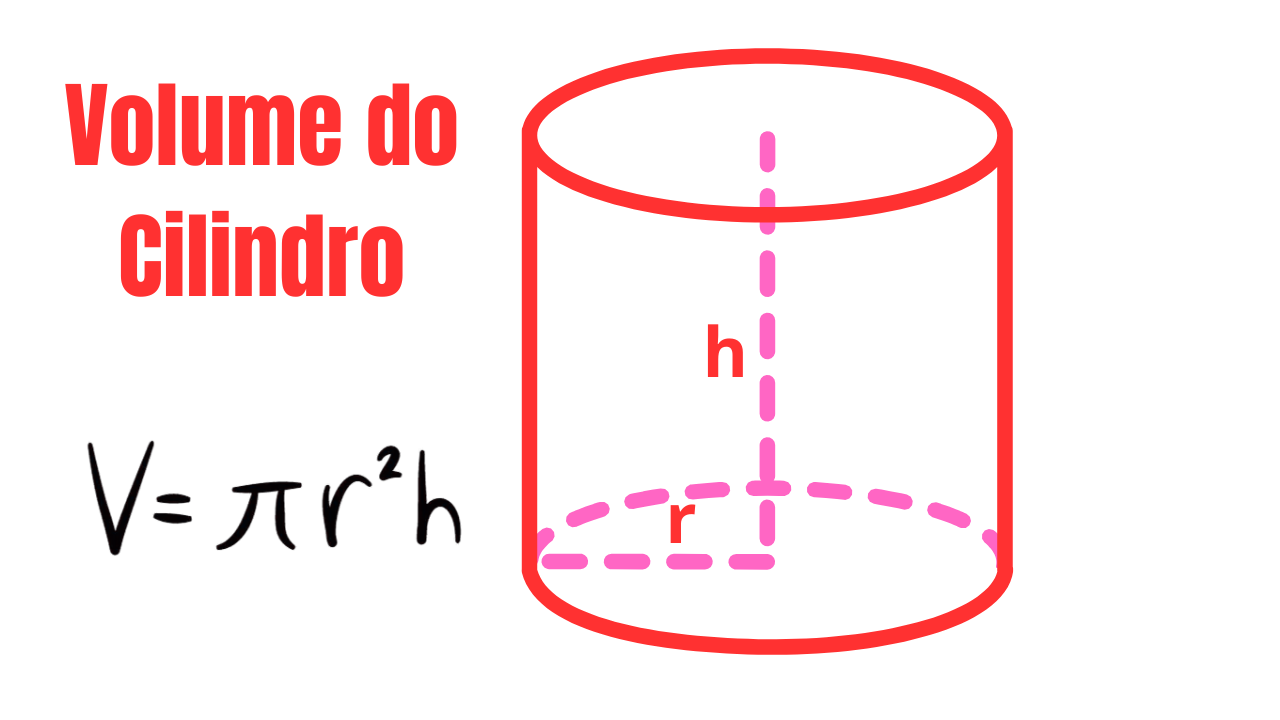
Definições em todo o artigo: \(r\) é o raio da base (raio do círculo da base). \(h\) é a altura do cilindro (distância perpendicular entre os planos das bases). Essas letras aparecem em todos os exemplos e exercícios.
Fórmula do volume
\(\displaystyle V=\pi r^2 h\)
Leitura: “área da base” \((\pi r^2)\) multiplicada pela “altura” \((h)\). Se \(r,h\) estiverem em centímetros, \(V\) sai em cm³ (1 L = 1 000 cm³; 1 m³ = 1 000 L).
Para ver outras fórmulas do sólido (área lateral/total e planificação), consulte Cilindro. Compare também com cone e esfera.
Por que a fórmula funciona?
- Prisma de base circular: todo prisma reto tem \(V=A_{\text{base}}\cdot h\). Para o cilindro, \(A_{\text{base}}=\pi r^2\), então \(V=\pi r^2 h\).
- Princípio de Cavalieri: se dois sólidos têm a mesma altura e cortes paralelos de mesma área em todos os níveis, têm o mesmo volume. As secções do cilindro por planos paralelos à base são círculos de área \(\pi r^2\).
Exemplos resolvidos
Exemplo 1 – Capacidade. Uma lata cilíndrica tem raio da base \(r=3{,}5\) cm e altura \(h=12\) cm. Qual é a capacidade em litros?
Ver solução
\(V=\pi r^2 h=\pi\cdot3{,}5^2\cdot12=147\pi\approx 461{,}8\ \text{cm}^3= \mathbf{0{,}462\ L}\).
Exemplo 2 – Encontrar o raio. Um frasco cilíndrico deve ter volume \(V=2\) L (= 2 000 cm³) e altura \(h=20\) cm. Determine o raio da base \(r\).
Ver solução
\(r=\sqrt{\dfrac{V}{\pi h}}=\sqrt{\dfrac{2000}{20\pi}}=\sqrt{\dfrac{100}{\pi}}\approx \mathbf{5{,}64\ \text{cm}}\).
Exemplo 3 – Tubo (cilindro oco). Um tubo tem raio externo \(R=6\) cm, raio interno \(r=5\) cm e altura \(h=10\) cm. Qual é o volume de metal?
Ver solução
\(V=\pi(R^2-r^2)h=\pi(36-25)\cdot10=110\pi\approx \mathbf{345{,}6\ \text{cm}^3}\).
Exemplo 4 – Aumento percentual. Uma lata teve o raio \(r\) aumentado em 10% e a altura \(h\) em 5%. De quanto o volume aumenta?
Ver solução
Fator volumétrico \(=1{,}10^2\cdot1{,}05=1{,}2715\). O volume aumenta cerca de 27,15%.
Exercício de Volume do Cilindro
Em todos os itens: \(r\) é o raio da base; \(h\) é a altura do cilindro. Use \(\pi\approx3{,}1416\) nas aproximações.
1) Uma lata cilíndrica tem raio da base \(r=4\) cm e altura \(h=10\) cm. Qual é a capacidade? A) 0,45 L B) 0,50 L C) 0,55 L D) 0,60 L
Solução
\(V=160\pi\approx 0{,}503\ \text{L}\) → B.
2) Um cilindro reto tem raio \(r=3\) cm e altura \(h=12\) cm. Qual a área do rótulo (apenas a superfície lateral)? A) 188,5 B) 226,2 C) 251,3 D) 282,7 (cm²)
Solução
\(A_L=2\pi rh=72\pi\approx 226{,}2\) → B.
3) Um vaso cilíndrico fechado possui raio \(r=5\) cm e altura \(h=8\) cm. Determine a área total externa. A) 377,0 B) 392,7 C) 408,4 D) 424,1 (cm²)
Solução
\(A_T=2\pi r(h+r)=130\pi\approx 408{,}4\) → C.
4) Um tanque tem raio \(r=1\) m e altura \(h=3\) m, mas está só na metade da altura. Qual o volume de água em litros? A) 3 770 B) 4 712 C) 5 240 D) 6 283
Solução
Metade do total: \(1{,}5\pi\ \text{m}^3\approx 4\,712\ \text{L}\) → B.
5) Uma chapa \(25\times20\) cm vira o rótulo de uma lata: usa-se 25 cm como circunferência da base, logo o raio é \(r=\tfrac{25}{2\pi}\) e a altura \(h=20\) cm. Qual o volume (cm³)? A) 905 B) 995 C) 1 050 D) 1 120
Solução
\(r\approx3{,}979\). \(V=\pi r^2h\approx 994{,}7\) → B.
6) Um cilindro oblíquo tem raio \(r=6\) cm e altura \(h=10\) cm (a geratriz é inclinada). Qual é o volume aproximado em litros? A) 0,95 L B) 1,13 L C) 1,26 L D) 1,41 L
Solução
O volume não muda com a inclinação: \(V=\pi r^2 h= \pi\cdot6^2\cdot10=360\pi\approx \mathbf{1{,}131\ \text{L}}\) → B.
7) Um reservatório cilíndrico deve armazenar 50 L. O raio da base é \(r=20\) cm. Qual a altura necessária (em cm)? A) 31,8 B) 35,0 C) 39,8 D) 45,0
Solução
\(V=50\,000\ \text{cm}^3=\pi r^2h\Rightarrow h=\frac{50\,000}{400\pi}= \frac{125}{\pi}\approx \mathbf{39{,}79\ \text{cm}}\) → C.
8) Uma lata tem raio \(r=6\) cm e altura \(h=12\) cm. Na planificação, qual deve ser a largura do rótulo (o comprimento do retângulo), em cm? A) 31,4 B) 34,6 C) 37,7 D) 43,98
Solução
Largura = circunferência da base \(=2\pi r=12\pi\approx \mathbf{37{,}70}\) → C.
9) Um depósito cilíndrico tem raio \(r=0{,}5\) m e altura \(h=1{,}2\) m. Qual o volume em litros? A) 785 B) 942 C) 1 000 D) 1 180
Solução
\(V=\pi r^2h=\pi\cdot0{,}25\cdot1{,}2=0{,}3\pi\ \text{m}^3\approx 0{,}9425\ \text{m}^3=\mathbf{942{,}5\ \text{L}}\) → B.
10) Misturam-se os conteúdos de duas latas: A com \(r=4\) cm e \(h=10\) cm; B com \(r=3\) cm e \(h=12\) cm. Qual o volume total em litros? A) 0,73 B) 0,79 C) 0,84 D) 0,92
Solução
\(V_A=160\pi\), \(V_B=108\pi\) cm³; total \(=268\pi\approx \mathbf{0{,}842\ \text{L}}\) → C.






















