Volume e Área da Esfera
A esfera é um dos principais corpos redondos. Todos os pontos da sua superfície estão à mesma distância do centro; essa distância é o raio \(r\). Para revisar definição e propriedades, veja o artigo Esfera. Para treinar, acesse Exercício Esfera. Compare com sólidos de faces planas: Cubo e Paralelepípedo.
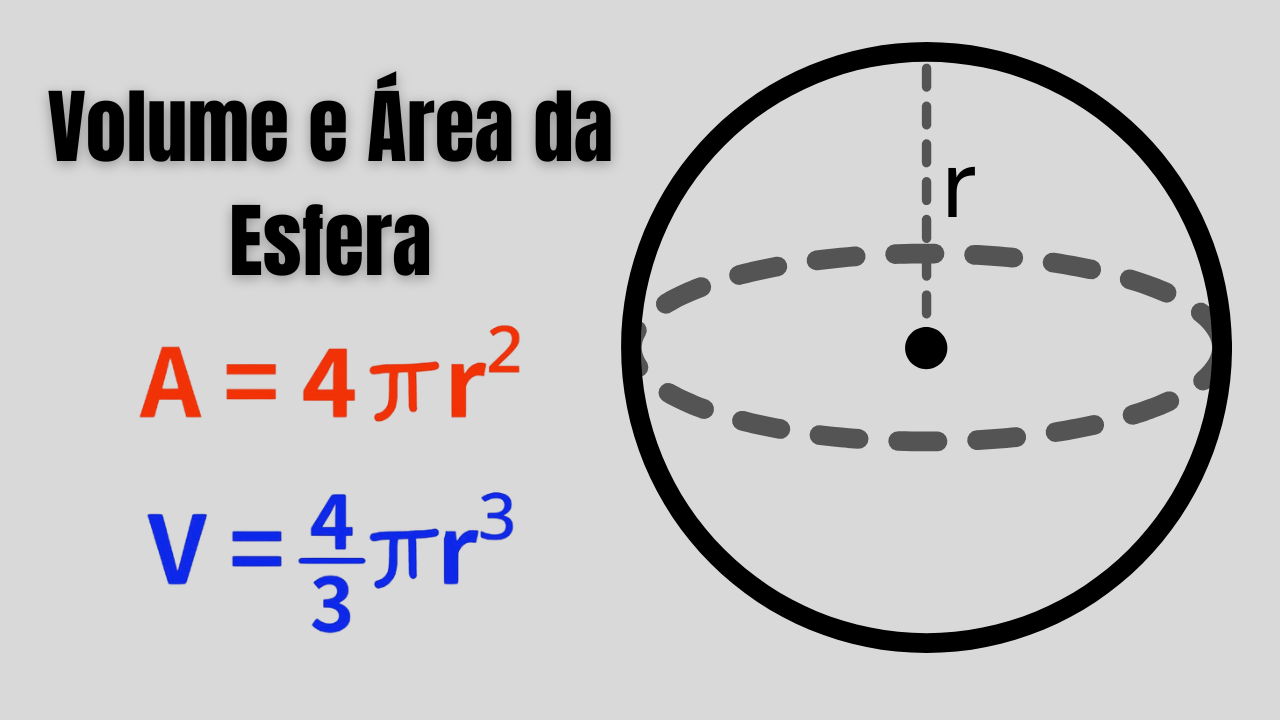
Fórmulas principais
- Unidades quadradas (cm², m²…)
- Com diâmetro \(d=2r\): \(A=\pi d^{2}\)
- Isolando \(r\): \( \displaystyle r=\sqrt{\dfrac{A}{4\pi}} \)
- Unidades cúbicas (cm³, m³…)
- Com diâmetro \(d\): \( \displaystyle V=\frac{\pi}{6}d^{3} \)
- Isolando \(r\): \( \displaystyle r=\sqrt[3]{\frac{3V}{4\pi}} \)
Intuição rápida
- De \(V\) para \(A\): \( \displaystyle \frac{d}{dr}\!\left(\frac{4}{3}\pi r^{3}\right)=4\pi r^{2}=A \). Ou seja, a variação do volume por unidade de raio é a própria área.
- Cavalieri: Comparando cortes da esfera com os de um cilindro de raio \(r\) e altura \(2r\) “vazado” por um cone, conclui-se \(V_{\text{esfera}}=\tfrac{2}{3}V_{\text{cilindro}}=\tfrac{4}{3}\pi r^{3}\).
- Escala: Se \(r\) é multiplicado por \(k\), então \(A\) multiplica por \(k^{2}\) e \(V\) por \(k^{3}\).
Unidades e conversões
Área em unidades quadradas; volume em unidades cúbicas. Em aplicações práticas: \(1\ \text{m}^{3}=1000\ \text{L}\).
Exemplos resolvidos
Exemplo 1. Para \(r=6\ \text{cm}\), calcule a área e o volume.
Exemplo 2. Uma esfera tem \(V=288\pi\ \text{cm}^{3}\). Encontre \(r\) e a área.
Exemplo 3. Esfera inscrita em um cubo de aresta \(10\ \text{cm}\): calcule \(A\) e \(V\).
Exercícios (múltipla escolha)
1) Direto. Uma esfera tem raio \(4\ \text{cm}\). O par correto (área, volume) é:
- \((64\pi\ \text{cm}^{2},\ 64\pi\ \text{cm}^{3})\)
- \((64\pi\ \text{cm}^{2},\ \tfrac{256}{3}\pi\ \text{cm}^{3})\)
- \((32\pi\ \text{cm}^{2},\ \tfrac{256}{3}\pi\ \text{cm}^{3})\)
- \((32\pi\ \text{cm}^{2},\ 64\pi\ \text{cm}^{3})\)
Ver solução
Resposta: B.
2) Com diâmetro. Se \(d=24\ \text{cm}\), então \(A\) e \(V\) valem, respectivamente:
- \(576\pi\ \text{cm}^{2}\) e \(2304\pi\ \text{cm}^{3}\)
- \(576\pi\ \text{cm}^{2}\) e \(\tfrac{\pi}{6}\cdot 24^{3}\)
- \( \pi d^{2}\) e \(\tfrac{\pi}{6}d^{3}\)
- Todas as anteriores estão corretas.
Ver solução
Resposta: D.
3) A partir do volume. Dada uma esfera com \(V=36\pi\ \text{cm}^{3}\), qual é a área?
- \(36\pi\ \text{cm}^{2}\)
- \(48\pi\ \text{cm}^{2}\)
- \(64\pi\ \text{cm}^{2}\)
- \(96\pi\ \text{cm}^{2}\)
Ver solução
Resposta: A.
4) Tanque esférico. Um reservatório esférico de raio \(1{,}2\ \text{m}\) será pintado externamente. Quanto se pinta (área) e qual sua capacidade (volume), aproximadamente?
- \(18{,}10\ \text{m}^{2}\) e \(7{,}24\ \text{m}^{3}\)
- \(9{,}05\ \text{m}^{2}\) e \(7{,}24\ \text{m}^{3}\)
- \(18{,}10\ \text{m}^{2}\) e \(3{,}62\ \text{m}^{3}\)
- \(9{,}05\ \text{m}^{2}\) e \(3{,}62\ \text{m}^{3}\)
Ver solução
Resposta: A.
5) Escala. Uma esfera B tem raio \(1{,}5\) vez o raio de uma esfera A. As razões \( \dfrac{A_B}{A_A} \) e \( \dfrac{V_B}{V_A} \) são, respectivamente:
- \(1{,}5\) e \(1{,}5\)
- \(2{,}25\) e \(3{,}375\)
- \(1{,}5^{2}\) e \(1{,}5^{2}\)
- \(2\) e \(3\)
Ver solução
Resposta: B.
Para continuar estudando
- Esfera — teoria completa.
- Exercício Esfera — listas com respostas e passo a passo.
- Corpos redondos — visão geral com comparações.
- Cubo • Paralelepipédedo — contraste de fórmulas e unidades.






















