Zero (Raiz) da Função do Segundo Grau: entenda Δ = b² − 4ac com exemplos
Os zeros (ou raízes) são os pontos em que a parábola corta o eixo x. Nesta página você aprende como o valor do discriminante decide o número de soluções reais e vê tudo aplicado passo a passo.
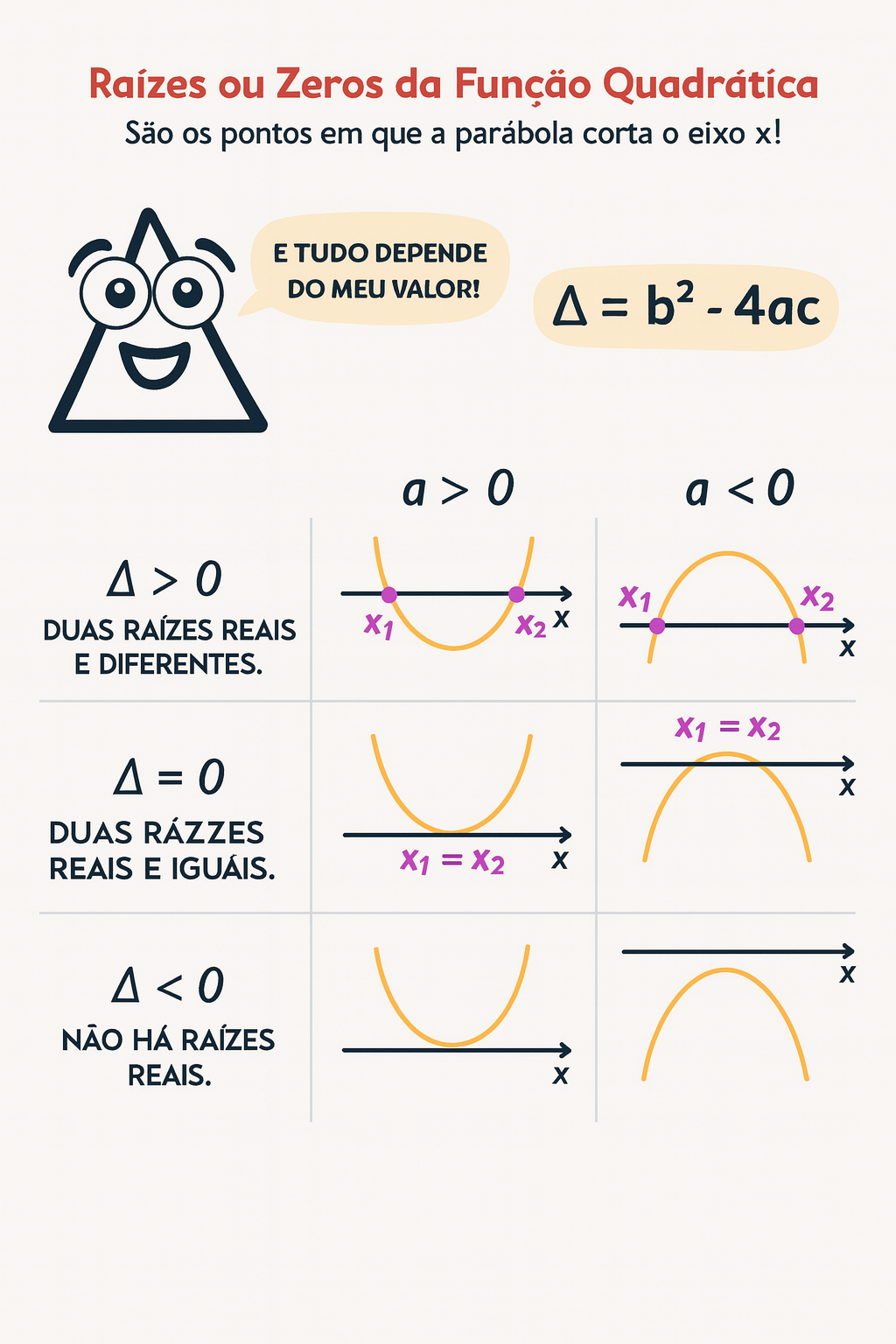
O que são raízes (zeros) da função quadrática?
A função do 2º grau tem forma geral \( f(x)=ax^2+bx+c \) com \(a\neq 0\). As raízes são os valores de \(x\) que tornam \(f(x)=0\). Para encontrá-las, usamos a fórmula de Bhaskara:
\[ x=\frac{-b\pm\sqrt{\Delta}}{2a}\quad \text{com}\quad \Delta=b^2-4ac. \]
O sinal de \( \Delta \) determina quantas raízes reais existem:
- Δ > 0: duas raízes reais e diferentes;
- Δ = 0: duas raízes reais e iguais (uma solução única);
- Δ < 0: não há raízes reais.
Caso 1 — Δ > 0
A parábola corta o eixo \(x\) em dois pontos distintos.
Caso 2 — Δ = 0
A parábola toca o eixo \(x\) apenas no vértice (raiz dupla).
Caso 3 — Δ < 0
A parábola não intercepta o eixo \(x\); as soluções são complexas (fora do conjunto dos reais).
Dica rápida
O coeficiente \(a\) decide se a parábola abre para cima (\(a>0\)) ou para baixo (\(a<0\)). Isso não muda a quantidade de raízes reais — quem manda é o Δ.
Continue estudando com estes recursos do Matemática Hoje 👇
Mapas Mentais de Matemática (visual e direto ao ponto) Matemática ENEM: questões por assunto Coleção com 10 eBooks de Matemática Banco de Questões de Matemática (para treinar muito!)📘 Tenha todas as fórmulas ao alcance
Baixe o eBook Fórmulas Matemática e revise Bhaskara, discriminante, funções, geometria, estatística e muito mais em um único PDF organizado.
Quero baixar o eBook de FórmulasExemplos resolvidos (passo a passo)
Exemplo 1 — Δ > 0 (duas raízes reais)
Encontre as raízes de \( f(x)=x^2-5x+6 \).
\[ \begin{aligned} a&=1,\quad b=-5,\quad c=6\\ \Delta&=b^2-4ac\\ &=(-5)^2-4\cdot1\cdot6\\ &=25-24\\ &=1\ (>0)\\[6pt] x&=\frac{-b\pm\sqrt{\Delta}}{2a}\\ &=\frac{-(-5)\pm\sqrt{1}}{2\cdot1}\\ &=\frac{5\pm1}{2} \end{aligned} \]
Logo, \(x_1=3\) e \(x_2=2\).
Exemplo 2 — Δ = 0 (raiz dupla)
Encontre as raízes de \( f(x)=x^2-4x+4 \).
\[ \begin{aligned} a&=1,\quad b=-4,\quad c=4\\ \Delta&=(-4)^2-4\cdot1\cdot4\\ &=16-16\\ &=0\\[6pt] x&=\frac{-b}{2a}\\ &=\frac{-(-4)}{2\cdot1}\\ &=\frac{4}{2}\\ &=2 \end{aligned} \]
Há apenas uma solução real: \(x_1=x_2=2\).
Exemplo 3 — Δ < 0 (sem raízes reais)
Considere \( f(x)=x^2+x+1 \).
\[ \begin{aligned} a&=1,\quad b=1,\quad c=1\\ \Delta&=1^2-4\cdot1\cdot1\\ &=1-4\\ &=-3\ (<0) \end{aligned} \]
Conclusão: a equação não possui raízes reais (as soluções são complexas).
Conclusão e próximos passos
Para dominar funções quadráticas, pratique bastante a identificação do Δ e a interpretação do gráfico. Depois, avance para tópicos relacionados e resolva exercícios de provas.













